题目内容
设不等式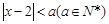 的解集为A,且
的解集为A,且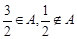
(Ⅰ)求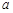 的值
的值
(Ⅱ)求函数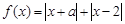 的最小值
的最小值
【答案】
(Ⅰ) (Ⅱ)
(Ⅱ) 的最小值为
的最小值为
【解析】 (Ⅰ)因为 ,且
,且 ,所以
,所以 ,且
,且
解得 ,又因为
,又因为 ,所以
,所以
(Ⅱ)因为
当且仅当 ,即
,即 时取得等号,所以
时取得等号,所以 的最小值为
的最小值为
不等式选讲如果如此题只考查绝对值不等式就算比较容易的题目,注意绝对值的三角不等式即可,当然也可通过讨论去掉绝对值号,当然还要注意均值和柯西不等式的应用。
【考点定位】本题考查绝对值不等式的基本内容,属于简单题。

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 的解集为A,不等式
的解集为A,不等式 的解集为B.如果
的解集为B.如果 ,求P的取值范围.
,求P的取值范围. 的解集为A,不等式
的解集为A,不等式 的解集为B.如果
的解集为B.如果 ,求P的取值范围.
,求P的取值范围.
 ,其中m是实数
,其中m是实数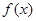 有零点,求m的取值范围;(7分)
有零点,求m的取值范围;(7分)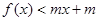 的解集为A,若
的解集为A,若 ,求m的取值范围。(7分)
,求m的取值范围。(7分) 的解集为A,不等式
的解集为A,不等式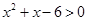 的解集为B.
的解集为B. 的解集为A∩B,求
的解集为A∩B,求 的值.
的值.