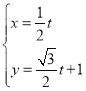题目内容
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数,
为参数,![]() ).
).
(Ⅰ)当![]() 时,若曲线
时,若曲线![]() 上存在
上存在![]() 两点关于点
两点关于点![]() 成中心对称,求直线
成中心对称,求直线![]() 的参数方程;
的参数方程;
(Ⅱ)在以原点为极点,![]() 轴的正半轴为极轴的极坐标系中,极坐标方程为
轴的正半轴为极轴的极坐标系中,极坐标方程为![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求实数
,求实数![]() 的值.
的值.
【答案】见解析
【解析】(Ⅰ)由题意,得曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),
消去参数,得![]() ,圆心坐标为
,圆心坐标为![]() .……………2分
.……………2分
∵曲线![]() 上存在
上存在![]() 两点关于点
两点关于点![]() 成中心对称,
成中心对称,
∴![]() ,则由
,则由![]() ,得
,得![]() ,
,
所以直线![]() 的倾斜角为
的倾斜角为![]() ,……………4分
,……………4分
所以直线![]() 的参数方程为
的参数方程为 ,即
,即 (
(![]() 为参数).……………6分
为参数).……………6分
(Ⅱ)消去曲线![]() 的参数方程中的参数得
的参数方程中的参数得![]() ,
,
圆心![]() 为
为![]() ,半径为
,半径为![]() .……………7分
.……………7分
又直线![]() 的极坐标方程可化为
的极坐标方程可化为![]() ,……………8分
,……………8分
由![]() ,代入上式,得直线的普通方程为
,代入上式,得直线的普通方程为![]() ,
,
所以 ,∴
,∴![]() .……………10分
.……………10分
【命题意图】本题考查直线的极坐标方程与直角坐标方程、圆的参数方程与普通方程的互化,以及直线与圆的位置关系,意在考查转化能力、运算求解能力.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目