Question

【题目】【2015高考天津，文20】已知函数

（I）求的单调区间;

（II）设曲线与轴正半轴的交点为P,曲线在点P处的切线方程为,求证:对于任意的正实数,都有;

（III）若方程有两个正实数根且,求证:.

Answer 1

【答案】（I） 的单调递增区间是 ,单调递减区间是;（II）见试题解析;（III）见试题解析.

【解析】

（I）由,可得 的单调递增区间是 ,单调递减区间是;（II）, ,证明 在单调递增,在单调递减,所以对任意的实数x, ,对于任意的正实数,都有;（III）设方程 的根为 ,可得,由在 单调递减,得 ,所以 .设曲线 在原点处的切线为 方程 的根为 ,可得 ,由 在在 单调递增,且 ,可得 所以 .

试题解析:（I）由,可得,当 ,即 时,函数 单调递增;当 ,即 时,函数 单调递减.所以函数 的单调递增区间是 ,单调递减区间是.

（II）设 ,则 , 曲线 在点P处的切线方程为 ,即,令 即 则.

由于在 单调递减,故在 单调递减,又因为,所以当时,,所以当时,,所以 在单调递增,在单调递减,所以对任意的实数x, ,对于任意的正实数,都有.

（III）由（II）知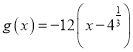 ,设方程 的根为 ,可得,因为在 单调递减,又由（II）知 ,所以 .类似的,设曲线 在原点处的切线为 可得 ,对任意的,有 即 .设方程 的根为 ,可得 ,因为 在 单调递增,且 ,因此, 所以 .