题目内容
函数f（x）=sin（ωx+φ）（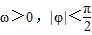
）的最小正周期是π，若其图象向右平移
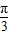个单位后得到的函数为奇函数，则函数f（x）的图象（ ）A．关于点
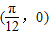对称B．关于点
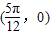对称C．关于直线
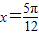对称D．关于直线
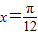对称
【答案】分析：由周期求出ω=2，故函数f（x）=sin（2x+φ），再根据图象向右平移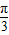
个单位后得到的函数 y=sin（2x-
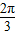+φ]是奇函数，可得φ=-
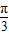，从而得到函数的解析式，从而求得它的对称性．
解答：解：由题意可得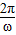
=π，解得ω=2，故函数f（x）=sin（2x+φ），其图象向右平移
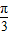个单位后得到的图象对应的函数为
y=sin[2（x-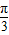
）+φ]=sin（2x-
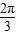+φ]是奇函数，故φ=-
，
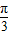故 函数f（x）=sin（2x-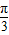
），故当
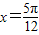时，函数f（x）=sin
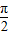=1，故函数f（x）=sin（2x-
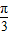） 关于直线
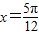对称，
故选C．
点评：本题主要考查诱导公式的应用，利用了y=Asin（ωx+φ）的图象变换规律，正弦函数的对称性，属于中档题．
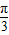个单位后得到的函数 y=sin（2x-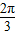+φ]是奇函数，可得φ=-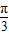，从而得到函数的解析式，从而求得它的对称性．解答：解：由题意可得
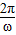=π，解得ω=2，故函数f（x）=sin（2x+φ），其图象向右平移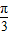个单位后得到的图象对应的函数为y=sin[2（x-
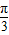）+φ]=sin（2x-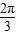+φ]是奇函数，故φ=-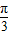，故 函数f（x）=sin（2x-
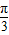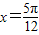），故当时，函数f（x）=sin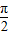=1，故函数f（x）=sin（2x-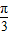） 关于直线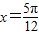对称，故选C．
点评：本题主要考查诱导公式的应用，利用了y=Asin（ωx+φ）的图象变换规律，正弦函数的对称性，属于中档题．
练习册系列答案
相关题目
函数f（x）=sin（ωx+?）（x∈R，ω＞0，0≤?＜2π）的部分图象如图，则