题目内容
已知函数f（x）=x2+alnx．
（1）当a=﹣2时，求函数f（x）的单调区间和极值；
（2）若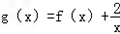
在[1，+∞）上是单调函数，求实数a的取值范围．
（1）当a=﹣2时，求函数f（x）的单调区间和极值；
（2）若
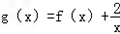在[1，+∞）上是单调函数，求实数a的取值范围．解：（1）易知，函数f（x）的定义域为（0，+∞）．
当a=﹣2时，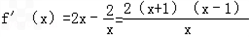
．
当x变化时，f'（x）和f（x）的值的变化情况如下表：
（2）由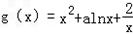
，得
．
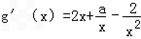又函数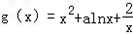
为[1，+∞）上单调函数，
①若函数g（x）为[1，+∞）上的单调增函数，
则g'（x）≥0在[1，+∞）上恒成立，
即不等式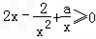
在[1，+∞）上恒成立．
也即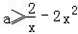
在[1，+∞）上恒成立，
而φ（x）=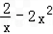
在[1，+∞）上的最大值为φ（0）=0，所以a≥0．
②若函数g（x）为[1，+∞）上的单调减函数，
根据①，在[1，+∞）上φ（x）max=φ（1）=0，φ（x）没有最小值．
所以g'（x）≤0在[1，+∞）上是不可能恒成立的．
综上，a的取值范围为[0，+∞）．
当a=﹣2时，
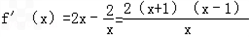．当x变化时，f'（x）和f（x）的值的变化情况如下表：
（2）由
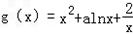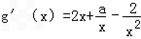，得．又函数
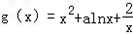为[1，+∞）上单调函数，①若函数g（x）为[1，+∞）上的单调增函数，
则g'（x）≥0在[1，+∞）上恒成立，
即不等式
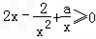在[1，+∞）上恒成立．也即
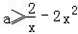在[1，+∞）上恒成立，而φ（x）=
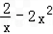在[1，+∞）上的最大值为φ（0）=0，所以a≥0．②若函数g（x）为[1，+∞）上的单调减函数，
根据①，在[1，+∞）上φ（x）max=φ（1）=0，φ（x）没有最小值．
所以g'（x）≤0在[1，+∞）上是不可能恒成立的．
综上，a的取值范围为[0，+∞）．
练习册系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|