题目内容
方程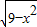 -k(x-3)-4=0有两个不同的解时,实数k的取值范围是( )
-k(x-3)-4=0有两个不同的解时,实数k的取值范围是( )A.(0,
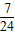 )
)B.(
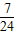 ,+∞)
,+∞)C.(
 ,
, )
)D.(
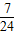 ,
, ]
]
【答案】分析:先将方程根的情况转化为一个半圆与一条直线交点的情况,再用数形结合,先求出相切时的斜率,再得到有两个交点的情况.
解答:解:将方程 -k(x-3)-4=0转化为:
-k(x-3)-4=0转化为:
半圆 ,与直线y=k(x-3)+4有两个不同交点.
,与直线y=k(x-3)+4有两个不同交点.
当直线与半圆相切时,有 ,即解得:k=
,即解得:k=
当半圆 与直线y=k(x-3)+4有两个不同交点时,
与直线y=k(x-3)+4有两个不同交点时,
因为直线y=k(x-3)+4一定过点(3,4),
所以由图象知直线过(-3,0)时直线的斜率k取最大值为 ,
,

所以k∈ .
.
故选D.
点评:本题主要考查用解析几何法来解决方程根的情况,关键是能够转化为一些特定的曲线才能用数形结合求解.
解答:解:将方程
 -k(x-3)-4=0转化为:
-k(x-3)-4=0转化为:半圆
 ,与直线y=k(x-3)+4有两个不同交点.
,与直线y=k(x-3)+4有两个不同交点.当直线与半圆相切时,有
 ,即解得:k=
,即解得:k=
当半圆
 与直线y=k(x-3)+4有两个不同交点时,
与直线y=k(x-3)+4有两个不同交点时,因为直线y=k(x-3)+4一定过点(3,4),
所以由图象知直线过(-3,0)时直线的斜率k取最大值为
 ,
,
所以k∈
 .
.故选D.
点评:本题主要考查用解析几何法来解决方程根的情况,关键是能够转化为一些特定的曲线才能用数形结合求解.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 -k(x-3)-4=0有两个不同的解时,实数k的取值范围是
-k(x-3)-4=0有两个不同的解时,实数k的取值范围是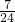 )
) ,
, )
)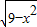 -k(x-3)-4=0有两个不同的解时,实数k的取值范围是( )
-k(x-3)-4=0有两个不同的解时,实数k的取值范围是( )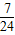 )
)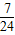 ,+∞)
,+∞) ,
, )
)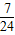 ,
, ]
]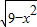 -k(x-3)-4=0有两个不同的解时,实数k的取值范围是( )
-k(x-3)-4=0有两个不同的解时,实数k的取值范围是( )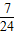 )
)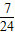 ,+∞)
,+∞) ,
, )
)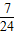 ,
, ]
]