题目内容
数列![]() 满足
满足![]() ,
,![]() .(1)求
.(1)求![]() 通项公式
通项公式![]() ;(2)令
;(2)令![]() ,数列
,数列![]() 前
前![]() 项和为
项和为![]() ,求证:当
,求证:当![]() 时,
时,![]() ;(3)证明:
;(3)证明:![]() .
.
(Ⅰ) ![]() (Ⅱ)见解析 (Ⅲ)见解析
(Ⅱ)见解析 (Ⅲ)见解析
解析:
(1)![]() ,两边同除以
,两边同除以![]() 得:
得:
![]() ∴
∴![]()
∴![]() 是首项为
是首项为![]() ,公比
,公比![]() 的等比数列…………4分
的等比数列…………4分
∴![]() ∴
∴![]()
(2)![]() ,当
,当![]() 时,
时,![]() ,
,![]() ………………5分
………………5分
两边平方得:![]()
![]()
![]() ……
……![]()
相加得:![]()
又![]()
![]() ∴
∴![]() …………9分
…………9分
(3)(数学归纳法)当![]() 时,显然成立
时,显然成立
当![]() 时,证明加强的不等式
时,证明加强的不等式![]()
假设当![]() 时命题成立,即
时命题成立,即![]()
则当![]() 时
时![]()
![]() ∴当
∴当![]() 时命题成立,故原不等式成立…14
时命题成立,故原不等式成立…14

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
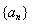
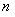
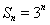
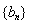
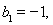
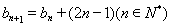

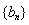
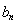
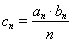
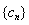
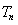
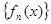 满足:
满足: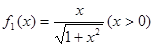 ,
,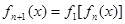
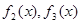 ;
;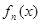 的表达式,并证明你的结论.
的表达式,并证明你的结论. 满足:
满足: ,
,
 ,
, ; (Ⅱ)令
; (Ⅱ)令 ,求数列
,求数列 的通项公式;
的通项公式; ,求证:
,求证: .
.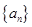 满足
满足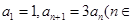 N*).
N*).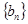 的各项均为正数,其前n项和为
的各项均为正数,其前n项和为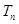 ,且
,且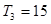 ,又
,又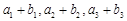 成等比数列,求
成等比数列,求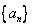 的首项为
的首项为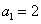 ,公比为
,公比为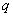 (
(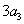 是
是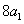 与
与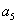 的等差中项;数列
的等差中项;数列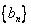 满足
满足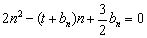 (
(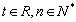 ).
).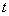 的值,使得数列
的值,使得数列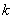 ,在
,在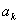 与
与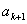 之间插入2共
之间插入2共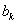 个,得到一个新数列
个,得到一个新数列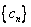 .设
.设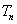 是数列
是数列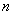 项和,试求满足
项和,试求满足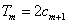 的所有正整数
的所有正整数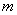 的值。
的值。