题目内容
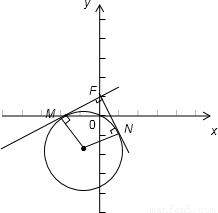
已知:点F是抛物线:x2=2py(p>0)的焦点,过F点作圆:(x+1)2+(y+2)2=5的两条切线互相垂直.(Ι)求抛物线的方程;
(Ⅱ)直线l:y=kx+b(k>0)交抛物线于A,B两点.
①若抛物线在A,B两点的切线交于P,求证:k-kPF>1;
②若B点纵坐标是A点纵坐标的4倍,A,B在y轴两侧,且
 ,求l的方程.
,求l的方程.
【答案】分析:(I)由题意可得:圆心、切点与点F形成的四边形为正方形,因为半径为 ,所以点F到圆心的距离为
,所以点F到圆心的距离为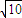 ,即可得
,即可得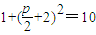 ,进而求出p的数值.
,进而求出p的数值.
(II)①设A,B两点的坐标分别为(x1,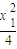 ),(x2,
),(x2,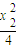 ),利用导数求出切线的斜率,写出两条切线的方程,求出交点P的坐标,进而求出kPF=
),利用导数求出切线的斜率,写出两条切线的方程,求出交点P的坐标,进而求出kPF=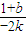 ,所以k-kPF=k-
,所以k-kPF=k-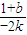 =k+
=k+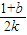 =
=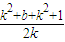 ,所以由基本不等式可得:k-kPF>
,所以由基本不等式可得:k-kPF>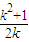 ≥1.
≥1.
②联立直线与抛物线的方程,利用根与系数的关系得到x1+x2=4k,x1x2=-4b,因为B点纵坐标是A点纵坐标的4倍,可得x2=-2x1.进而得到b=8k2.因为 ,结合题意可得
,结合题意可得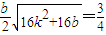 ,进而得到k=
,进而得到k= ,b=
,b= .
.
解答:解:(I)由题意可得:过F点作圆:(x+1)2+(y+2)2=5的两条切线互相垂直,切点分别为M,N.
所以由圆心、切点与点F形成的四边形为正方形,
因为半径为 ,
,
所以点F到圆心的距离为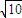 ,即可得
,即可得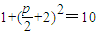 ,
,
解得:p=2或者p=-10(舍去),
所以抛物线的方程为x2=4y.
(II)①设A,B两点的坐标分别为(x1,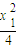 ),(x2,
),(x2,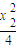 ),
),
因为抛物线的方程为x2=4y,
所以y′= x.
x.
所以切线AP为: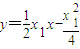 …①
…①
切线BP的方程为: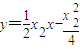 …②,
…②,
由①②可得点P的坐标为(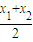 ,
,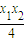 ).
).
联立直线l:y=kx+b与抛物线的方程的方程可得:x2-4kx-4b=0,
所以△=16k2+16b>0,x1+x2=4k,x1x2=-4b,
所以可得点P的坐标为(2k,-b),
所以kPF=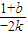 ,
,
所以k-kPF=k-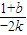 =k+
=k+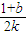 =
=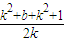 >
>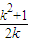 ,
,
所以由基本不等式可得:k-kPF>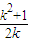 ≥1.
≥1.
所以k-kPF>1.
②设A,B两点的坐标分别为(x1,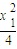 ),(x2,
),(x2,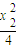 ),
),
由题意可得:联立直线l:y=kx+b与抛物线的方程的方程可得:x2-4kx-4b=0,
所以△=16k2+16b>0,x1+x2=4k,x1x2=-4b,…①
因为B点纵坐标是A点纵坐标的4倍,
所以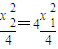 ,即x22=4x12.
,即x22=4x12.
因为A,B在y轴两侧,
所以x2=-2x1…②
由①②可得:b=8k2…③..
又因为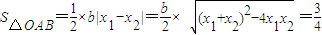 ,
,
所以结合①整理可得: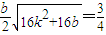 …④,
…④,
所以由③④可得:k= ,b=
,b= .
.
所以l的方程为: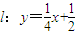 .
.
点评:解决此类问题的关键是熟练掌握抛物线的标准方程,以及直线与抛物线的位置关系,并且熟练利用利用数形结合的数学思想解决数学问题.
 ,所以点F到圆心的距离为
,所以点F到圆心的距离为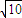 ,即可得
,即可得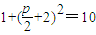 ,进而求出p的数值.
,进而求出p的数值.(II)①设A,B两点的坐标分别为(x1,
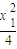 ),(x2,
),(x2,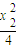 ),利用导数求出切线的斜率,写出两条切线的方程,求出交点P的坐标,进而求出kPF=
),利用导数求出切线的斜率,写出两条切线的方程,求出交点P的坐标,进而求出kPF=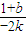 ,所以k-kPF=k-
,所以k-kPF=k-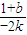 =k+
=k+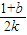 =
=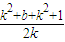 ,所以由基本不等式可得:k-kPF>
,所以由基本不等式可得:k-kPF>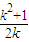 ≥1.
≥1.②联立直线与抛物线的方程,利用根与系数的关系得到x1+x2=4k,x1x2=-4b,因为B点纵坐标是A点纵坐标的4倍,可得x2=-2x1.进而得到b=8k2.因为
 ,结合题意可得
,结合题意可得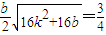 ,进而得到k=
,进而得到k= ,b=
,b= .
.解答:解:(I)由题意可得:过F点作圆:(x+1)2+(y+2)2=5的两条切线互相垂直,切点分别为M,N.
所以由圆心、切点与点F形成的四边形为正方形,
因为半径为
 ,
,所以点F到圆心的距离为
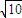 ,即可得
,即可得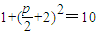 ,
,解得:p=2或者p=-10(舍去),
所以抛物线的方程为x2=4y.

(II)①设A,B两点的坐标分别为(x1,
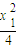 ),(x2,
),(x2,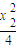 ),
),因为抛物线的方程为x2=4y,
所以y′=
 x.
x.所以切线AP为:
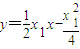 …①
…①切线BP的方程为:
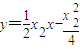 …②,
…②,由①②可得点P的坐标为(
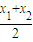 ,
,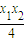 ).
).联立直线l:y=kx+b与抛物线的方程的方程可得:x2-4kx-4b=0,
所以△=16k2+16b>0,x1+x2=4k,x1x2=-4b,
所以可得点P的坐标为(2k,-b),
所以kPF=
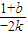 ,
,所以k-kPF=k-
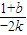 =k+
=k+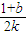 =
=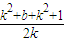 >
>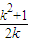 ,
,所以由基本不等式可得:k-kPF>
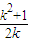 ≥1.
≥1.所以k-kPF>1.
②设A,B两点的坐标分别为(x1,
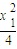 ),(x2,
),(x2,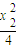 ),
),由题意可得:联立直线l:y=kx+b与抛物线的方程的方程可得:x2-4kx-4b=0,
所以△=16k2+16b>0,x1+x2=4k,x1x2=-4b,…①
因为B点纵坐标是A点纵坐标的4倍,
所以
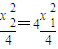 ,即x22=4x12.
,即x22=4x12.因为A,B在y轴两侧,
所以x2=-2x1…②
由①②可得:b=8k2…③..
又因为
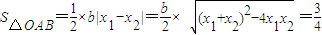 ,
,所以结合①整理可得:
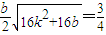 …④,
…④,所以由③④可得:k=
 ,b=
,b= .
.所以l的方程为:
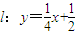 .
.点评:解决此类问题的关键是熟练掌握抛物线的标准方程,以及直线与抛物线的位置关系,并且熟练利用利用数形结合的数学思想解决数学问题.

练习册系列答案
相关题目