题目内容
如图1,在直角梯形ABCD中,AB∥CD,AB⊥AD,且AB=AD=
CD=1.现以AD为一边向形外作正方形ADEF,然后沿边AD将正方形ADEF翻折,使平面ADEF与平面ABCD互相垂直,如图2.
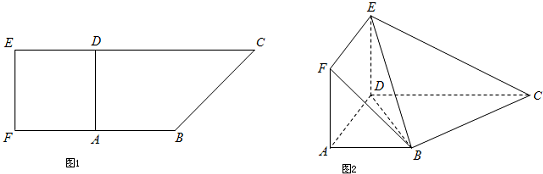
(1)求证:平面BDE⊥平面BEC;
(2)求平面ABCD与平面EFB所成锐二面角的大小.
| 1 |
| 2 |

(1)求证:平面BDE⊥平面BEC;
(2)求平面ABCD与平面EFB所成锐二面角的大小.

(1)证明:在正方形ADEF中,ED⊥AD.
又因为平面ADEF⊥平面ABCD,且平面ADEF∩平面ABCD=AD,
所以ED⊥平面ABCD.
所以ED⊥BC.
在直角梯形ABCD中,AB=AD=1,CD=2,可得BC=
| 2 |
在△BCD中,BD=BC=
| 2 |
所以BD2+BC2=CD2.
所以BC⊥BD.
所以BC⊥平面BDE.
因为BC?平面BEC,所以平面BDE⊥平面BEC;
(2)过E作EG⊥BC,连接DG,则
∵AB⊥AD,沿边AD将正方形ADEF翻折,使平面ADEF与平面ABCD互相垂直,
∴ED⊥平面ABCD
∴∠EGD为平面ABCD与平面EFB所成角
∵AB=AD=
| 1 |
| 2 |
∴DG=
| 2 |
∴tan∠EGD=
| 1 | ||
|
| ||
| 2 |
∴∠EGD=arctan
| ||
| 2 |

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目


 (2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.
(2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.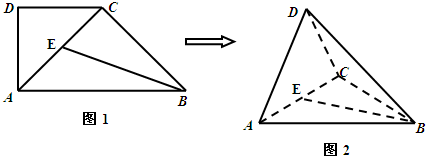 (1)求证:DA⊥BC;
(1)求证:DA⊥BC;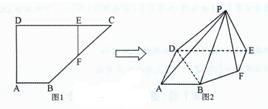 如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2.
如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2.