题目内容
已知正项等比数列{an}，a1＝2，又bn＝log2an，且数列{bn}的前7项和T7最大，T7≠T6，且T7≠T8，则数列{an}的公比q的取值范围是( )(A)
＜q＜
(B)
＜q＜
(C)q＜或q＞ (D)q＞
或q＜
B.∵bn＝log2an，而{a
n}是以a1＝2为首项，q为公比的等比数列，∴bn＝log2an＝log2(a1qn－1)＝1＋(n－1)log2q.
∴bn＋1－bn＝log2q.∴{bn}是等差数列，由于前7项之和T7最大，且T7≠T6，所以有
解得－
＜log2q＜－
，
即＜q＜.故选B.
练习册系列答案
相关题目
的前n项和为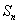
，若数列
有如下运算和结论：① 
是等比数列；
，使
则
.其中正确的结论有 .(请填上所有正确结论的序号)
的前
项和为
且满足
则
中最大的项为 （ ）
，把数列
的各项排列成如下的三角形状，记
表示第
行的第
= ( ) A.
B.
C. 
D.
是圆
：
上的两个点，
是
线段上的动点，当
的面积最大时，则
的最大值是（ ） 
D. 
为单位向量，且
，
=1，则
； ⑵若
=0，则
； ⑷若
，则必有
； ⑸若
，则
已知△ABC为等边三角形，AB=2．设点P，Q满足
，
，λ∈R．若
=﹣
，则λ=（ ）
|
| A． |
| B． |
| C． |
| D． |
|
求得
的值为
（D）