题目内容
(本小题满分13分)
已知定义在R上的函数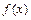 满足:①对任意的
满足:①对任意的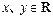 ,都有
,都有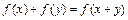 ;②当
;②当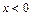 时,有
时,有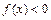 .
.
(1)利用奇偶性的定义,判断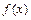 的奇偶性;
的奇偶性;
(2)利用单调性的定义,判断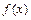 的单调性;
的单调性;
(3)若关于x的不等式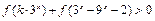 在
在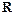 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.
已知定义在R上的函数
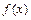 满足:①对任意的
满足:①对任意的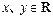 ,都有
,都有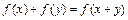 ;②当
;②当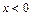 时,有
时,有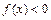 .
.(1)利用奇偶性的定义,判断
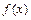 的奇偶性;
的奇偶性;(2)利用单调性的定义,判断
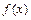 的单调性;
的单调性;(3)若关于x的不等式
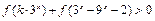 在
在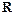 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.解析:(1)令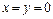 ,得
,得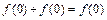 ,得
,得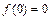 .将“y”用“
.将“y”用“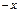 ”代替,得
”代替,得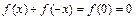 ,即
,即 ,∴
,∴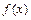 为奇函数.
为奇函数.
(2)设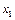 、
、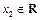 ,且
,且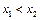 ,则
,则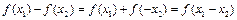 .
.
∵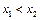 ,∴
,∴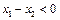 ,∴
,∴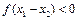 ,即
,即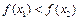 ,∴
,∴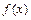 在R上是增函数.
在R上是增函数.
(3)方法1 由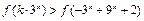 得
得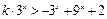 ,即
,即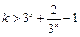 对
对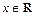 有解.∵
有解.∵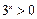 ,∴由对勾函数
,∴由对勾函数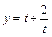 在
在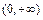 上的图象知当
上的图象知当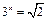 ,即
,即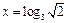 时,
时,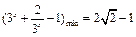 ,故
,故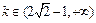 .
.
方法2 由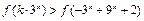 得
得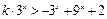 ,即
,即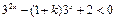 对
对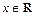 有解.令
有解.令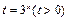 ,则
,则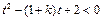 对
对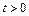 有解.
有解.
记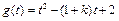 ,则
,则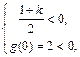 或
或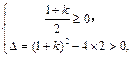 解得
解得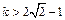 .
.
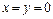 ,得
,得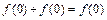 ,得
,得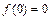 .将“y”用“
.将“y”用“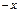 ”代替,得
”代替,得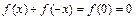 ,即
,即 ,∴
,∴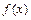 为奇函数.
为奇函数.(2)设
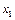 、
、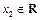 ,且
,且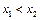 ,则
,则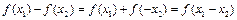 .
.∵
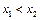 ,∴
,∴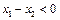 ,∴
,∴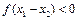 ,即
,即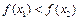 ,∴
,∴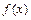 在R上是增函数.
在R上是增函数.(3)方法1 由
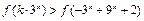 得
得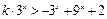 ,即
,即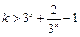 对
对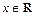 有解.∵
有解.∵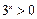 ,∴由对勾函数
,∴由对勾函数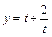 在
在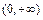 上的图象知当
上的图象知当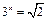 ,即
,即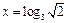 时,
时,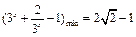 ,故
,故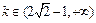 .
.方法2 由
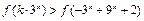 得
得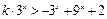 ,即
,即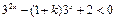 对
对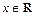 有解.令
有解.令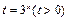 ,则
,则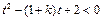 对
对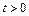 有解.
有解.记
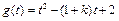 ,则
,则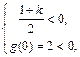 或
或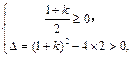 解得
解得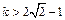 .
.略

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
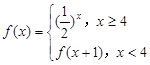 ,则
,则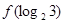 等于
等于



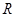 上的函数
上的函数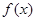 满足
满足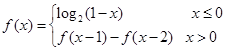 ,则
,则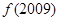 的值为( )
的值为( )
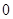

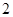
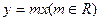 与函数
与函数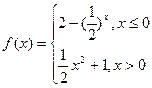 的图象恰有三个不同的公共点,
的图象恰有三个不同的公共点,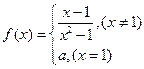 在
在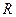 上连续,则
上连续,则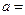 ( )
( )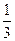
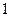
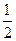
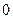
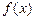 ,
,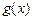 ,在公共定义域内,规定
,在公共定义域内,规定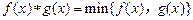 ,若
,若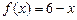 ,
,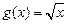 ,则
,则
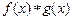 的最大值为_______________.
的最大值为_______________.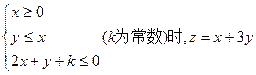 的最大值12,则k的值为 。
的最大值12,则k的值为 。