题目内容
16.已知角α的顶点在原点,始边为x轴的非负半轴,若角α的终边过点$P(x,-\sqrt{2})$,且$cosα=\frac{{\sqrt{3}}}{6}x$(x≠0),判断角α所在的象限,并求sinα和tanα的值.分析 利任意角的三角函数的定义求得x的值,分类讨论求得sinα和tanα的值.
解答 解:依题意,点P到原点O的距离为$r=|{OP}|=\sqrt{{x^2}+{{(-\sqrt{2})}^2}}=\sqrt{{x^2}+2}$,则$cosα=\frac{x}{r}=\frac{x}{{\sqrt{{x^2}+2}}}=\frac{{\sqrt{3}}}{6}x$,
∵x≠0,∴x2+2=12,∴x2=10,$x=±\sqrt{10}$,
∴$r=2\sqrt{3}$,所以P在第三或第四象限.
当点P在第三象限时,$x=-\sqrt{10}$,$y=-\sqrt{2}$,则$sinα=\frac{y}{r}=-\frac{{\sqrt{6}}}{6}$,$tanα=\frac{y}{x}=\frac{{\sqrt{5}}}{5}$;
当点P在第四象限时,$x=\sqrt{10}$,$y=-\sqrt{2}$,则$sinα=\frac{y}{r}=-\frac{{\sqrt{6}}}{6}$,$tanα=\frac{y}{x}=-\frac{{\sqrt{5}}}{5}$.
点评 本题主要考查任意角的三角函数的定义,两点间的距离公式的应用,体现了分类讨论的数学思想.属于基础题.

练习册系列答案
相关题目
6.一个三位自然数abc的百位,十位,个位上的数字依次为a,b,c,当且仅当a<b且c<b时称为“凸数”.若a,b,c∈{5,6,7,8,9},且a,b,c互不相同,任取一个三位数abc,则它为“凸数”的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
11.已知函数f(x)满足f(x)+f(-x)=0,在[-1,0]上为单调增函数,又α,β为锐角三角形二个内角,则( )
| A. | f(cosα)>f(cosβ) | B. | f(sinα)>f(sinβ) | C. | f(sinα)<f(cosβ) | D. | f(sinα)>f(cosβ) |
8.两个复数z1=a1+b1i,z2=a2+b2i,(a1,b1,a2,b2都是实数且z1≠0,z2≠0),对应的向量在同一直线上的充要条件是( )
| A. | $\frac{b_1}{a_1}•\frac{b_2}{a_2}=-1$ | B. | a1a2+b1b2=0 | ||
| C. | $\frac{b_1}{a_1}=\frac{b_2}{a_2}$ | D. | a1b2=a2b1 |
5.已知函数$y=sin\frac{x}{2}+\sqrt{3}cos\frac{x}{2},x∈R$.的最大值为( )
| A. | 1+$\sqrt{3}$ | B. | 2 | C. | 1 | D. | $\sqrt{3}+\frac{1}{2}$ |
6.($\sqrt{2}$x-1)5的展开式中第3项的系数是( )
| A. | -20$\sqrt{2}$ | B. | 20 | C. | -20 | D. | 20$\sqrt{2}$ |
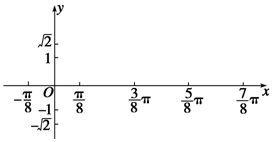 已知曲线y=Asin(ωx+φ) (A>0,ω>0)上的一个最高点的坐标为($\frac{π}{8}$,$\sqrt{2}$),此点到相邻最低点间的曲线与x轴交于点 ($\frac{3}{8}$π,0),若φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).
已知曲线y=Asin(ωx+φ) (A>0,ω>0)上的一个最高点的坐标为($\frac{π}{8}$,$\sqrt{2}$),此点到相邻最低点间的曲线与x轴交于点 ($\frac{3}{8}$π,0),若φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).