题目内容
设![]() ,
,![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴上的点,且
轴上的点,且![]()
![]()
![]() ,动点
,动点![]() 满足:
满足:![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过定点![]() 任意作一条直线
任意作一条直线![]() 与曲线
与曲线![]() 交与不同的两点
交与不同的两点![]() 、
、![]() ,问在
,问在![]() 轴上是否存在一定点
轴上是否存在一定点![]() ,使得直线
,使得直线![]() 、
、![]() 的倾斜角互补?若存在,求出
的倾斜角互补?若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
(1)![]() .
.
(2)存在点![]() 符合题意.
符合题意.
解析:
(1)设![]() ,则
,则![]() 、
、![]() ,
,![]()
又![]() ,
,![]() ,即
,即![]() .
.
(2)设直线![]() 的方程为:
的方程为:![]() ,
,![]() 、
、![]()
假设存在点![]() 满足题意,则
满足题意,则![]() ,
,
 ,即
,即![]() ,
,![]() ,
,
![]() ,又
,又![]()
![]()
![]() ,
,
由于![]() ,则
,则![]()
对不同的![]() 值恒成立,即
值恒成立,即![]() 对不同的
对不同的![]() 值恒成立,
值恒成立,
则![]() ,即
,即![]() ,故存在点
,故存在点![]() 符合题意.
符合题意.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
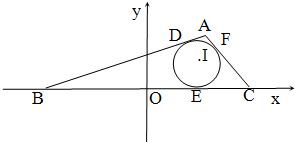 如图,△ABC的内切圆与三边AB、BC、CA的切点分别为D、E、F,已知B(-
如图,△ABC的内切圆与三边AB、BC、CA的切点分别为D、E、F,已知B(-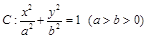 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为 ,离心率为
,离心率为 ,在
,在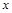 轴负半轴上有一点
轴负半轴上有一点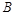 ,且
,且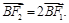
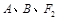 三点的圆恰好与直线
三点的圆恰好与直线 相切,求椭圆C的方程;
相切,求椭圆C的方程;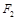 作斜率为
作斜率为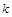 的直线
的直线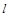 与椭圆C交于
与椭圆C交于 两点,在
两点,在 ,使得以
,使得以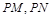 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.
 :
:
 的左、右焦点分别为
的左、右焦点分别为
 ,过点
,过点 垂直的直线交
垂直的直线交 轴负半轴于点
轴负半轴于点 ,且
,且 ,若过
,若过 三点的圆恰好与直线
三点的圆恰好与直线 :
: 相切. 过定点
相切. 过定点 的直线
的直线 与椭圆
与椭圆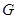 ,
, 两点(点
两点(点 ,
,
 ,在
,在 ,使得以
,使得以 ,
, 为邻边的平行四边形是菱形. 如果存在,求出
为邻边的平行四边形是菱形. 如果存在,求出 的取值范围,如果不存在,请说明理由;
的取值范围,如果不存在,请说明理由; 满足
满足 ,求
,求 的取值范围.
的取值范围. 的左,右两个焦点分别为
的左,右两个焦点分别为 ,短轴的上端点为
,短轴的上端点为 ,短轴上的两个三等分点为
,短轴上的两个三等分点为 ,且
,且 为正方形,若过点
为正方形,若过点 轴上的一个截距为
轴上的一个截距为 ,则此椭圆方程的方程为 ▲
.
,则此椭圆方程的方程为 ▲
.