题目内容
设函数 。
。
(Ⅰ)求 的极大值点与极小值点;
的极大值点与极小值点;
(Ⅱ)求 在区间
在区间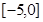 上的最大值与最小值。
上的最大值与最小值。
【答案】
解:(Ⅰ) 。
。
令 ,解得
,解得 。1分
。1分
∵ 的单调递增区间
的单调递增区间 ,单调递减区间
,单调递减区间 ,
, 。2分
。2分
∴ 的极大值点
的极大值点
 ,极小值点
,极小值点 。3分
。3分
(Ⅱ)列表
|
|
|
|
|
|
0 |
|
|
|
- |
0 |
+ |
|
|
|
|
↘ |
极小值 |
↗ |
|
5分
当 时,
时, ,
,
当 时,
时, ,
,
当 时,
时, 。
。
∴在区间 上的最大值为63,最小值为0。7分
上的最大值为63,最小值为0。7分
【解析】本试题主要是考查了函数的极值和最值问题的运用。
(1)先求解导数,然后判定函数的单调性,利用极值的概念可知道饿到第一问的结论。
(2)在第一问的基础上,进一步比较端点值的函数值域极值的大小关系得到最值。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目















 ,
, 的值;
的值; 的最小值。
的最小值。 )
)
 上是单调函数,求
上是单调函数,求 的取值范围。
的取值范围。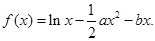
 时,求
时,求 的最大值;
的最大值; ,(
,( ),其图象上任意一点
),其图象上任意一点 处切线的斜率
处切线的斜率 ≤
≤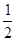 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
, 的最小正周期以及单调增区间;
的最小正周期以及单调增区间; 时,求
时,求 ,求
,求 的值.
的值. 。
。 的单调区间;
的单调区间; ,不等式
,不等式 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;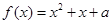 在区间[0, 2] 恰有两个不等实根,求a的取值范围。
在区间[0, 2] 恰有两个不等实根,求a的取值范围。