题目内容
(理科)如图所示,ABCD-A1B1C1D1是棱长为a的正方体,M是棱A1B1的中点,N是棱A1D1的中点.(1)求直线AN与平面BB1D1D所成角的大小;
(2)求B1到平面ANC的距离.

【答案】分析:(1)以D为坐标原点,建立空间直角坐标系,求出平面BB1D1D的一个法量,利用 和此法向量夹角求解.向量知识求解.
和此法向量夹角求解.向量知识求解.
(2)求出平面ANC的一个方法向量,B1到平面ANC的距离等于 在此法向量方向上投影的绝对值.利用向量知识求解.
在此法向量方向上投影的绝对值.利用向量知识求解.
解答:解:以D为坐标原点,建立如图所示的坐标系.

则A(a,0,0),N( ,0,a),C(0,a,0),B1 (a,a,a)
,0,a),C(0,a,0),B1 (a,a,a)
 =(-
=(- ,0,a),
,0,a),
(1)易知平面BB1D1D的一个法量 =(-a,a,0)----2分
=(-a,a,0)----2分
 ,----------------------------------2分
,----------------------------------2分
设直线AN与平面BB1D1D所成角为θ
 ------------------------------1分
------------------------------1分
 ,
,
直线AN与平面BB1D1D所成角为 -------1分
-------1分
(2)设平面ANC的一个方法向量
 ,
,
取u=2, -----3分
-----3分
所以 =
= -----------------------------2分
-----------------------------2分
=a----------------------------------------2分
点评:本题考查空间直角和平面所成就的计算,点面距离求解,考查空间想象能力、计算能力.
 和此法向量夹角求解.向量知识求解.
和此法向量夹角求解.向量知识求解.(2)求出平面ANC的一个方法向量,B1到平面ANC的距离等于
 在此法向量方向上投影的绝对值.利用向量知识求解.
在此法向量方向上投影的绝对值.利用向量知识求解.解答:解:以D为坐标原点,建立如图所示的坐标系.

则A(a,0,0),N(
 ,0,a),C(0,a,0),B1 (a,a,a)
,0,a),C(0,a,0),B1 (a,a,a) =(-
=(- ,0,a),
,0,a),(1)易知平面BB1D1D的一个法量
 =(-a,a,0)----2分
=(-a,a,0)----2分 ,----------------------------------2分
,----------------------------------2分设直线AN与平面BB1D1D所成角为θ
 ------------------------------1分
------------------------------1分 ,
,
直线AN与平面BB1D1D所成角为
 -------1分
-------1分(2)设平面ANC的一个方法向量

 ,
,取u=2,
 -----3分
-----3分所以
 =
= -----------------------------2分
-----------------------------2分=a----------------------------------------2分
点评:本题考查空间直角和平面所成就的计算,点面距离求解,考查空间想象能力、计算能力.

练习册系列答案
相关题目
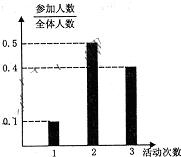 (理科)某中学号召学生在2010年春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
(理科)某中学号召学生在2010年春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生,他们参加活动的次数统计如图所示. (2010•陕西高考理科•T7)若某空间几何体的三视图如图所示,则该几何体的体积是( )
(2010•陕西高考理科•T7)若某空间几何体的三视图如图所示,则该几何体的体积是( ) (理科做)如图所示已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD且PA=1.建立适当的空间坐标系,利用空间向量求解下列问题:
(理科做)如图所示已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD且PA=1.建立适当的空间坐标系,利用空间向量求解下列问题: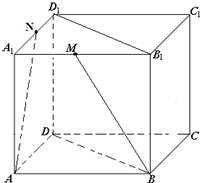 (理科)如图所示,ABCD-A1B1C1D1是棱长为a的正方体,M是棱A1B1的中点,N是棱A1D1的中点.
(理科)如图所示,ABCD-A1B1C1D1是棱长为a的正方体,M是棱A1B1的中点,N是棱A1D1的中点.