题目内容
2.已知数列{an}中,a1=2,$\frac{{a}_{n}}{{a}_{n+1}}$=2,若an≥$\frac{3}{64}$,则n的最大取值为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 利用等比数列的通项公式可得:an,再利用不等式的性质即可得出.
解答 解:∵a1=2,$\frac{{a}_{n}}{{a}_{n+1}}$=2,
∴数列{an}是等比数列,首项为2,公比为$\frac{1}{2}$.
∴an=2×$(\frac{1}{2})^{n-1}$,
∵an≥$\frac{3}{64}$,
∴2×$(\frac{1}{2})^{n-1}$≥$\frac{3}{64}$,
∵a6=$\frac{4}{64}$,a7=$\frac{2}{64}$,
∴n的最大值为6.
故选:B.
点评 本题考查了等比数列的通项公式、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
13.已知O为坐标原点,$\overrightarrow{OA}$=(1,2),$\overrightarrow{OB}$=(-2,-1),则$\frac{|\overrightarrow{AB}|}{\overrightarrow{OA}•\overrightarrow{OB}}$=( )
| A. | -$\frac{3\sqrt{2}}{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | -$\frac{3\sqrt{2}}{4}$ | D. | $\frac{3\sqrt{2}}{4}$ |
10.已知实数x,y满足$\left\{\begin{array}{l}{x≥1}\\{x+y≤2}\\{x-y≤2}\end{array}\right.$,若不等式y≥ax-3恒成立,则实数a的取值范围为( )
| A. | (-∞,$\frac{3}{2}$] | B. | (-∞,4] | C. | [$\frac{3}{2}$,2] | D. | [2,4] |
7.若执行如图所示的程序,输出的结果为48,则判断框中应填入的条件为( )


| A. | i≥6? | B. | i>6? | C. | i≥4? | D. | i>4? |
12.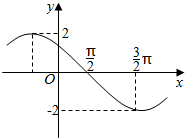 已知f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象的一部分如图所示,则f(x)解析式是( )
已知f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象的一部分如图所示,则f(x)解析式是( )
 已知f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象的一部分如图所示,则f(x)解析式是( )
已知f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象的一部分如图所示,则f(x)解析式是( )| A. | f(x)=2sin($\frac{1}{2}$x-$\frac{π}{4}$) | B. | f(x)=2sin($\frac{1}{2}$x+$\frac{3π}{4}$) | C. | f(x)=2sin(2x-$\frac{π}{4}$) | D. | f(x)=2sin(2x+$\frac{3π}{4}$) |
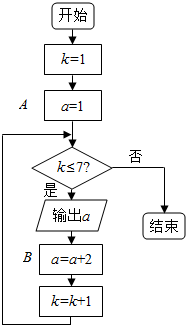 按图所示的程序框图操作:
按图所示的程序框图操作: