题目内容
已知lg2=a,lg3=b,则lg215=______;(试用a,b表示)
∵lg2=a,lg3=b,
∴log215=log23+log25=log23+log2
=
+log210-1=
+
-1
=
+
-1=
.
故答案为
.
∴log215=log23+log25=log23+log2
| 10 |
| 2 |
=
| lg3 |
| lg2 |
| lg3 |
| lg2 |
| 1 |
| lg2 |
=
| b |
| a |
| 1 |
| a |
| 1+b-a |
| a |
故答案为
| 1+b-a |
| a |

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
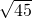 的值为 ________.
的值为 ________. 的值为 .
的值为 .