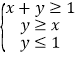Question

【题目】已知动圆过点且与直线相切，圆心的轨迹为曲线.

（1）求曲线的方程；

（2）若，是曲线上的两个点且直线过的外心，其中为坐标原点，求证：直线过定点.

Answer 1

【答案】(1) (2)证明见解析

【解析】

（1）根据题意，设点，由半径相等建立关系式，化简即可求得解析式；

（2）可判断直线斜率一定存在，设直线的方程为，联立直线与抛物线方程求得关于的韦达定理，再由直线过的外心，可得，即，结合前式的韦达定理表示的关系式解方程可求参数，即可求定点

（1）设点，则，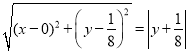

平方整理得：，

∴曲线的方程为.

（2）证明：由题意可知直线的斜率一定存在，否则不与曲线有两个交点.

设的方程为，设点，，联立方程

得，

则得，，

由得：，.

.

.

∵直线过的外心，其中为坐标原点，∴.

∴，

∴，，

解得，当时，满足.

∴直线过定点.