题目内容
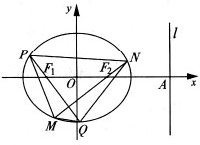 如图,F1、F2分别为椭圆
如图,F1、F2分别为椭圆 的焦点,椭圆的右准线l与x轴交于A点,若F1(-1,0),且
的焦点,椭圆的右准线l与x轴交于A点,若F1(-1,0),且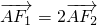 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过F1、F2作互相垂直的两直线分别与椭圆交于P、Q、M、N四点,求四边形PMQN面积的取值范围.
解:(I) 由F1(-1,0)得c=1,∴A点坐标为(a2,0);…(2分)
∵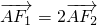 ,∴F2是AF1的中点,∴a2=3,b2=2
,∴F2是AF1的中点,∴a2=3,b2=2
∴椭圆方程为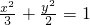 …(5分)
…(5分)
(II)当直线MN与PQ中有一条与x轴垂直时,四边形PMQN面积 ;…(6分)
;…(6分)
当直线PQ,MN均与x轴不垂直时,不妨设PQ:y=k(x+1)(k≠0),
联立 代入消去y得(2+3k2)x2+6k2x+(3k2-6)=0
代入消去y得(2+3k2)x2+6k2x+(3k2-6)=0
设P(x1,y1),Q(x2,y2)则 …(8分)
…(8分)
∴ ,同理
,同理
∴四边形PMQN面积 …(10分)
…(10分)
令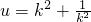 ,则
,则 ,则S是以u为变量的增函数
,则S是以u为变量的增函数
所以当k=±1,u=2时, ,∴
,∴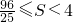
综上可知, ,∴四边形PMQN面积的取值范围为
,∴四边形PMQN面积的取值范围为 …(13分)
…(13分)
分析:(I) 先确定A点坐标为(a2,0),利用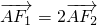 ,可得F2是AF1的中点,由此可求椭圆方程;
,可得F2是AF1的中点,由此可求椭圆方程;
(II)当直线MN与PQ中有一条与x轴垂直时,四边形PMQN面积 ;当直线PQ,MN均与x轴不垂直时,设直线PQ、MN的方程与椭圆方程联立,求得|PQ|,|MN|,表示出四边形PMQN面积,再换元,即可求得四边形PMQN面积的取值范围.
;当直线PQ,MN均与x轴不垂直时,设直线PQ、MN的方程与椭圆方程联立,求得|PQ|,|MN|,表示出四边形PMQN面积,再换元,即可求得四边形PMQN面积的取值范围.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查四边形面积的计算,直线方程与椭圆方程联立,正确表示四边形的面积是关键.
∵
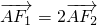 ,∴F2是AF1的中点,∴a2=3,b2=2
,∴F2是AF1的中点,∴a2=3,b2=2∴椭圆方程为
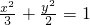 …(5分)
…(5分)(II)当直线MN与PQ中有一条与x轴垂直时,四边形PMQN面积
 ;…(6分)
;…(6分)当直线PQ,MN均与x轴不垂直时,不妨设PQ:y=k(x+1)(k≠0),
联立
 代入消去y得(2+3k2)x2+6k2x+(3k2-6)=0
代入消去y得(2+3k2)x2+6k2x+(3k2-6)=0设P(x1,y1),Q(x2,y2)则
 …(8分)
…(8分)∴
 ,同理
,同理
∴四边形PMQN面积
 …(10分)
…(10分)令
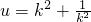 ,则
,则 ,则S是以u为变量的增函数
,则S是以u为变量的增函数所以当k=±1,u=2时,
 ,∴
,∴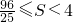
综上可知,
 ,∴四边形PMQN面积的取值范围为
,∴四边形PMQN面积的取值范围为 …(13分)
…(13分)分析:(I) 先确定A点坐标为(a2,0),利用
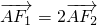 ,可得F2是AF1的中点,由此可求椭圆方程;
,可得F2是AF1的中点,由此可求椭圆方程;(II)当直线MN与PQ中有一条与x轴垂直时,四边形PMQN面积
 ;当直线PQ,MN均与x轴不垂直时,设直线PQ、MN的方程与椭圆方程联立,求得|PQ|,|MN|,表示出四边形PMQN面积,再换元,即可求得四边形PMQN面积的取值范围.
;当直线PQ,MN均与x轴不垂直时,设直线PQ、MN的方程与椭圆方程联立,求得|PQ|,|MN|,表示出四边形PMQN面积,再换元,即可求得四边形PMQN面积的取值范围.点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查四边形面积的计算,直线方程与椭圆方程联立,正确表示四边形的面积是关键.

练习册系列答案
相关题目
 如图,F1,F2分别为椭圆
如图,F1,F2分别为椭圆 如图,F1、F2分别为椭圆
如图,F1、F2分别为椭圆 如图,F1,F2分别为双曲线
如图,F1,F2分别为双曲线 如图,F1、F2分别为椭圆
如图,F1、F2分别为椭圆 的左、右焦点,点P在椭圆上,△POF2是面积
的左、右焦点,点P在椭圆上,△POF2是面积 的正三角形,则
的正三角形,则 的值是
的值是