题目内容
已知命题 是偶函数;命题q:?a∈R,g(x)=ax2+2x-1在(0,+∞)上单调递减,则下列结论正确的是
是偶函数;命题q:?a∈R,g(x)=ax2+2x-1在(0,+∞)上单调递减,则下列结论正确的是
- A.p,q都是真命题
- B.p是真命题,q是假命题
- C.p,q都是假命题
- D.p是假命题,q是真命题
B
分析:利用偶函数的定义可判断命题p为真;分类讨论可判断命题q是假命题.
解答:∵ ,∴命题
,∴命题 是偶函数为真命题;
是偶函数为真命题;
g(x)=ax2+2x-1,
当a=0时,g(x)=2x-1在(0,+∞)上单调递增;
当a>0时,函数的对称轴为x=- <0,g(x)=ax2+2x-1在(0,+∞)上单调递增;
<0,g(x)=ax2+2x-1在(0,+∞)上单调递增;
当a<0时,函数的对称轴为x=- >0,g(x)=ax2+2x-1在(0,-
>0,g(x)=ax2+2x-1在(0,- )上单调递增,在(-
)上单调递增,在(- ,+∞)上单调递减,故命题q是假命题
,+∞)上单调递减,故命题q是假命题
故选B.
点评:本题考查命题真假的判断,考查学生的计算能力,属于基础题.
分析:利用偶函数的定义可判断命题p为真;分类讨论可判断命题q是假命题.
解答:∵
 ,∴命题
,∴命题 是偶函数为真命题;
是偶函数为真命题;g(x)=ax2+2x-1,
当a=0时,g(x)=2x-1在(0,+∞)上单调递增;
当a>0时,函数的对称轴为x=-
 <0,g(x)=ax2+2x-1在(0,+∞)上单调递增;
<0,g(x)=ax2+2x-1在(0,+∞)上单调递增;当a<0时,函数的对称轴为x=-
 >0,g(x)=ax2+2x-1在(0,-
>0,g(x)=ax2+2x-1在(0,- )上单调递增,在(-
)上单调递增,在(- ,+∞)上单调递减,故命题q是假命题
,+∞)上单调递减,故命题q是假命题故选B.
点评:本题考查命题真假的判断,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
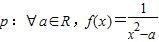 是偶函数;命题q:?a∈R,g(x)=ax2+2x-1在(0,+∞)上单调递减,则下列结论正确的是( )
是偶函数;命题q:?a∈R,g(x)=ax2+2x-1在(0,+∞)上单调递减,则下列结论正确的是( )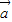 ,
,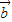 满足
满足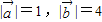 ,且
,且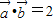 ,则
,则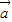 与
与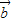 的夹角为
的夹角为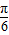 ;
;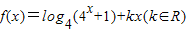 是偶函数,函数
是偶函数,函数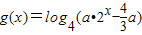 ,若函数f(x)的图象与函数g(x)的图象有且只有一个公共点,则实数a的取值范围是(1,+∞).
,若函数f(x)的图象与函数g(x)的图象有且只有一个公共点,则实数a的取值范围是(1,+∞).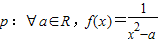 是偶函数;命题q:?a∈R,g(x)=ax2+2x-1在(0,+∞)上单调递减,则下列结论正确的是( )
是偶函数;命题q:?a∈R,g(x)=ax2+2x-1在(0,+∞)上单调递减,则下列结论正确的是( )