题目内容

已知AD是△ABC的中线，
AD
=λ
AB
+μ
AC 
(λ， μ∈R)，那么λ+μ=
1
1
；若∠A=120°，
AB
•
AC
=-2，则|
AD
|的最小值是
1
1
．
分析：由题意可得，
BD
+
CD
=
0
，而由
AD
=
AB
+
BD
，
AD
=
AC
+
CD
可得，结合已知，可求λ，μ
由
AB
•
AC
=|
AB
|•|
AC
|cos120°=bccos120°=-2可得bc=4，由|
AD
|=
1
2
|
AB
+
AC
|=
1
2
(
AB
+
AC
)2
=
1
2
AB
2+
AC
2+2
AB
•
AC
=
1
2
c2+b2-4
，由基本不等式可求
解答：解：D是△ABC边BC的中点
∴
BD
=-
CD
即
BD
+
CD
=
0

∵
AD
=
AB
+
BD

AD
=
AC
+
CD

∴2
AD
=
AB
+
AC
+
BD
+
CD
=
AB
+
AC

即
AD
=
1
2
(
AB
+
AC
)
∵
AD
=λ
AB
+μ
AC 
(λ， μ∈R)，
∴λ=μ=
1
2

∴λ+μ=1
∵
AD
=
1
2
(
AB
+
AC
)，
AB
•
AC
=-2
又
AB
•
AC
=|
AB
|•|
AC
|cos120°=bccos120°=-2
∴bc=4
∴|
AD
|=
1
2
|
AB
+
AC
|=
1
2
(
AB
+
AC
)2
=
1
2
AB
2+
AC
2+2
AB
•
AC

=
1
2
c2+b2-4
≥
1
2
2bc-4
=1（当且仅当b=c时取等号）
|
AD
|的最小值为1
故答案为：1；1
点评：本题主要考查了向量加法的三角形法则及向量的数量积的基本运算，向量数量积的运算性质，基本不等式求解最值，属于基本知识的综合应用．
练习册系列答案
相关题目
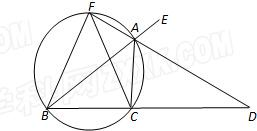精英家教网如图，已知AD是△ABC的外角∠EAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F，连接FB、FC．
（1）求证：FB=FC；
（2）求证：FB2=FA•FD；
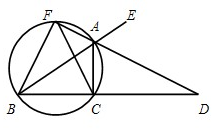选修4-1：几何证明选讲
已知AD是△ABC的外角∠EAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F，连接FB，FC．
（1）求证：FB=FC；
（2）若AB是△ABC外接圆的直径，∠EAC=120°，BC=6，求AD的长．
在△ABC中，∠A=120°
（Ⅰ）若三边长构成公差为4的等差数列，求△ABC的面积；
（Ⅱ）已知AD是△ABC的中线，若
AB
•
AC
=-2，求|
AD
|的最小值．
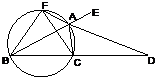（几何证明选讲选做题）已知AD是△ABC的外角∠EAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F，连接FB，FC．
（1）求证：FB=FC；
（2）若AB是△ABC外接圆的直径，∠EAC=120°，BC=3
3
，求AD的长．
已知AD是△ABC的中线，若∠A=120°，
AB
•
AC
=-2，则|
AD
|的最小值是
1
1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网