题目内容
已知AD是△ABC的中线，若∠A=120°，
•
=-2，则|
|的最小值是
| AB |
| AC |
| AD |
1
1
．分析：利用向量的数量积公式，及三角形中线向量的表示，利用基本不等式，即可求|
|的最小值．
| AD |
解答：解：∵
•
=-2=|
||
|cosA，∠A=120°，----------------------（7分）
∴|
||
|=4----------------------------------（8分）
∵|
|=
（
+
），
∴|
|2=
（|
|2+|
|2+2
•
）=
（|
|2+|
|2-4）
≥
（2|
||
|-4）=1---------------（10分）
∴|
|min=1----------------------------------（12分）
故答案为：1．
| AB |
| AC |
| AB |
| AC |
∴|
| AB |
| AC |
∵|
| AD |
| 1 |
| 2 |
| AB |
| AC |
∴|
| AD |
| 1 |
| 4 |
| AB |
| AC |
| AB |
| AC |
| 1 |
| 4 |
| AB |
| AC |
≥
| 1 |
| 4 |
| AB |
| AC |
∴|
| AD |
故答案为：1．
点评：本题考查向量的数量积，基本不等式，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
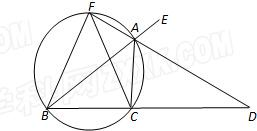如图，已知AD是△ABC的外角∠EAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F，连接FB、FC．
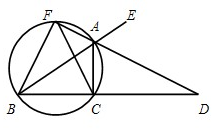选修4-1：几何证明选讲
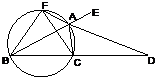（几何证明选讲选做题）已知AD是△ABC的外角∠EAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F，连接FB，FC．