题目内容
已知椭圆
+
=1上的两点A、B关于直线y=kx-1对称，F2是椭圆的右焦点，若|AF2|+|BF2|=
，AB中点到椭圆左准线的距离为
，求椭圆与直线方程．
| x2 |
| a2 |
| 25y2 |
| 9a2 |
| 8a |
| 5 |
| 3 |
| 2 |
分析：题中有较多的与椭圆几何性质有关的线段，由此设左焦点为F1，将|AF2|+|BF2|=
，利用椭圆的第一定义得出|AF1|+|BF1|=4a-
=
．
AB将AB中点到椭圆左准线的距离为
，利用椭圆的第二定义得出|AF1|+|BF1|=e(|，
由此求出a=1，确定椭圆方程为：x2+
=1，左准线方程x=-
，再利用差分法求k．
| 8a |
| 5 |
| 8a |
| 5 |
| 12a |
| 5 |
AB将AB中点到椭圆左准线的距离为
| 3 |
| 2 |
由此求出a=1，确定椭圆方程为：x2+
| 25y2 |
| 9 |
| 5 |
| 4 |
解答：解：设左焦点为F1，则|AF1|=2a-|AF2|，|BF1|=2a-|BF2|，
∴|AF1|+|BF1|=4a-
=
．
过A，B，AB中点M分别向左准线作垂线，垂足分别为A1，B1，M1，
而e=
，|AF1|+|BF1|=e(|，
∴
=
，则a=1
从而椭圆方程为：x2+
=1，左准线方程x=-
，
设A（x1，y1），B（x2，y2），
则
．
则作差有
=-
而AB中点(x0，y0)，x0=-
+
=
，y0=
-1，
=
=
=KAB=-
，
求得k=
，故所求直线方程为：y=
x-1．
∴|AF1|+|BF1|=4a-
| 8a |
| 5 |
| 12a |
| 5 |
过A，B，AB中点M分别向左准线作垂线，垂足分别为A1，B1，M1，
而e=
| 4 |
| 5 |
∴
| 12a |
| 5 |
| 12 |
| 5 |
从而椭圆方程为：x2+
| 25y2 |
| 9 |
| 5 |
| 4 |
设A（x1，y1），B（x2，y2），
则
|
则作差有
| y1-y2 |
| x1-x2 |
| 9(x1+x2) |
| 25(y1+y2) |
而AB中点(x0，y0)，x0=-
| 5 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| k |
| 4 |
| y1-y2 |
| x1-x2 |
| -9x0 |
| 25y0 |
| 9 |
| 25(k-4) |
| 1 |
| k |
求得k=
| 25 |
| 4 |
| 25 |
| 4 |
点评：本题考查椭圆的标准方程，椭圆的两种定义，直线与椭圆的位置关系，考查差分法的运用，属于中档题
练习册系列答案
53随堂测系列答案
相关题目
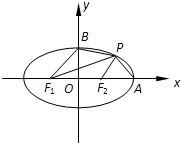如图，已知椭圆