题目内容
已知函数![]() 。
。
(1)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若直线![]() 对任意的
对任意的![]() 都不是曲线
都不是曲线![]() 的切线,求
的切线,求![]() 的取值范围;
的取值范围;
(3)设![]() ,求
,求![]() 的最大值
的最大值![]() 的解析式。
的解析式。
解:(1)∵当a=1时![]() ,
,![]()
又![]() ,
, ![]()
![]() 在
在![]() 处的切线的斜率为-3且过点
处的切线的斜率为-3且过点![]()
∴![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ………(3分)
………(3分)
(2)∵![]()
![]() ∴要使直线
∴要使直线![]() =0对任意的
=0对任意的![]() 总不是曲线
总不是曲线![]()
![]() 的切线,当且仅当-1<-3a, ∴
的切线,当且仅当-1<-3a, ∴![]() . ………(6分)
. ………(6分)
(3)因![]() 在[-1,1]上为偶函数,故只求在 [0,1]上最大值,
在[-1,1]上为偶函数,故只求在 [0,1]上最大值,
① 当![]() 时,
时,![]()
![]() ,
,![]() 在
在![]() 上单调递增且
上单调递增且![]() ,
,
∴![]() ,∴
,∴![]() .
.
② 当![]() 时
时 ![]()
i当![]() ,即
,即![]() 时
时![]() ,
,![]() 在
在![]() 上单调递增,此时
上单调递增,此时![]()
ii当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调减,在
上单调减,在![]() 上单调增.
上单调增.
10 当![]() 即
即![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,故
上单调递减,故![]() .
.
20当![]() 即
即![]() 时,
时,
(ⅰ)当![]() 即
即![]() 时,
时, ![]()
(ⅱ) 当![]() 即
即![]() 时,
时,![]()
综上

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 ,
,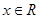 .
.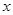 为何值时,
为何值时,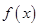 取得最大值,并求出其最大值;
取得最大值,并求出其最大值; ,
,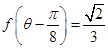 ,求
,求 的值.
的值.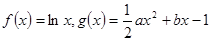 ,
, 且
且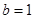 时,证明:对
时,证明:对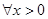 ,
,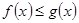 ;
;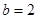 ,且
,且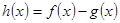 存在单调递减区间,求
存在单调递减区间,求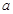 的取值范围;
的取值范围;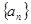 ,若存在常数
,若存在常数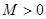 ,
,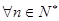 ,都有
,都有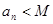 ,则称数列
,则称数列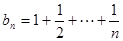 ,试判断数列
,试判断数列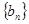 是否有上界.
是否有上界.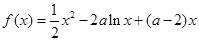 ,
, .
. 时,求函数
时,求函数 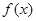 的最小值;
的最小值; 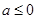 时,讨论函数
时,讨论函数 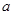 ,对任意的
,对任意的
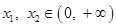 ,且
,且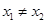 ,有
,有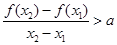 ,恒成立,若存在求出
,恒成立,若存在求出