题目内容
已知函数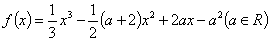 。
。
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若a=4,y=f(x)的图像与直线y=m有三个交点,求m的取值范围。
已知函数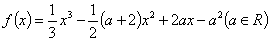 。
。
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若a=4,y=f(x)的图像与直线y=m有三个交点,求m的取值范围。
解:(Ⅰ)函数 的定义域为
的定义域为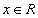 ,
,

①当a=2时, 恒成立,
恒成立, 在R上是增函数。
在R上是增函数。
②当a<2时,f'(x)≥0在(-∞,a]和[2,+∞)上恒成立,f'(x)≤0在
[a,2]上恒成立.
∴a<2时f(x)的增区间为(-∞,a]和[2,+∞),f(x)的减区间为[a,2].
③当a>2时,f'(x)≥0在(-∞,2]和[a,+∞)上恒成立,f'(x)≤0在
[2,a]上恒成立,
∴a>2时,f(x)的增区间为(-∞,2]和[a,+∞),f(x)的减区间为[2,a].
(Ⅱ)若a=4,由(Ⅰ)可得f(x)在(-∞,2]上单调递增,在[4,+∞)上单调递增,在[2,4]上单调递减。——————10分
f(x)极小值=f(4)= , ----11分 f(2)极大值=f(2)=
, ----11分 f(2)极大值=f(2)= ,
,
∴y=f(x)的图像与直线y=m有三个交点时m的取值范围是( ,
, )。
)。

练习册系列答案
相关题目
 ,a=10,则边长c的取值范围是( )
,a=10,则边长c的取值范围是( ) B.(10,+∞)
B.(10,+∞)
 在R是单调函数,则实数
在R是单调函数,则实数 的取值范围是( )
的取值范围是( ) B、
B、
 D、
D、
 ,则当n=k+1时左端应在n=k的基础上加上________________________
,则当n=k+1时左端应在n=k的基础上加上________________________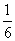 B.
B.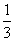 C.
C.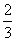 D.
D.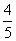
 =(-2,1),
=(-2,1), =(-2,-3),则
=(-2,-3),则 B. 0 C.
B. 0 C.