题目内容
如图,已知过原点O从x轴正方向出发逆时针旋转240°得到射线t,点A(x,y)在射线t上(x<0,y<0=,设|OA|=m,又知点B在射线y=0(x<0=上移动,设P为第三象限内的动点,若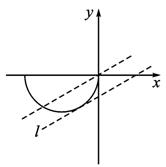
(1)试问点P的轨迹是什么曲线?
(2)已知直线l的斜率为![]() ,若直线l与曲线C有两个不同的交点M,N,设线段MN的中点为Q,求点Q的横坐标的取值范围.
,若直线l与曲线C有两个不同的交点M,N,设线段MN的中点为Q,求点Q的横坐标的取值范围.
解:(1)设点A(x1,![]() x1),B(x1,0),P(x,y).
x1),B(x1,0),P(x,y).
∵![]() ⊥
⊥![]() ,∴x=x2.
,∴x=x2.
∵|OA|=m,
∴![]() =|2x1|=m,
=|2x1|=m,
∵点A在第三象限,∴x1<0,

∴x1=-![]() ,A(-
,A(-![]() ,-
,-![]() m).
m).
∵![]() ·
·![]() +|
+|![]() |2=
|2=![]() ·
·![]() ,
,
即[-(x+![]() ,y+
,y+![]() m)]·(0,-y)+(x+
m)]·(0,-y)+(x+![]() ,
,![]() m)2
m)2
=(![]() ,
,![]() m)·(x+
m)·(x+![]() ,y+
,y+![]() m),
m),
整理得(x+![]() )2+y2=
)2+y2=![]() (x<0,y<0),
(x<0,y<0),
∴点P的轨迹是圆的一部分.
(2)设点Q(x0,y0),l:y=![]() x+b,
x+b,
M(x1,y1),N(x2,y2),

![]()
![]() x2+(
x2+(![]() +b)x+b2=0,
+b)x+b2=0,
Δ=0时,b=-![]() m或
m或![]() m(舍),
m(舍),
∴b∈(-![]() m,0),
m,0),
x0=![]() =-
=-![]() ,
,
∴x0∈(-![]() m,
m,![]() m).
m).

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
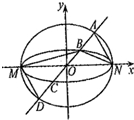 (2013•湖北)如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A,B,C,D,记
(2013•湖北)如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A,B,C,D,记

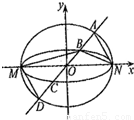 如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A,B,C,D,记
如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A,B,C,D,记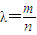 ,△BDM和△ABN的面积分别为S1和S2.
,△BDM和△ABN的面积分别为S1和S2.