题目内容
已知F1,F2是椭圆的两个焦点,在椭圆上满足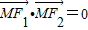 的M点有四个,则椭圆离心率的取值范围是______
的M点有四个,则椭圆离心率的取值范围是______
【答案】分析:由F1,F2是椭圆的两个焦点,在椭圆上满足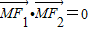 ,知,
,知,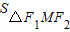 =b2,设M点纵坐标为h,则h=
=b2,设M点纵坐标为h,则h=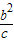 ,由椭圆上满足
,由椭圆上满足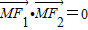 的M点有四个,得
的M点有四个,得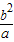 <
<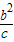 <b,由此能求出椭圆离心率的取值范围.
<b,由此能求出椭圆离心率的取值范围.
解答: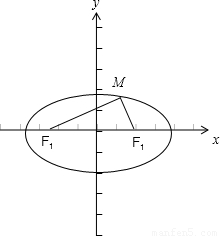 解:∵F1,F2是椭圆的两个焦点,在椭圆上满足
解:∵F1,F2是椭圆的两个焦点,在椭圆上满足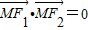 ,
,
∴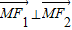 ,
,
∴∠F1MF2=90°,
∴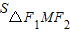 =b2,
=b2,
设M点纵坐标为h,则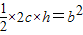 ,
,
∴h=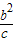 ,
,
∵椭圆上满足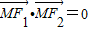 的M点有四个,
的M点有四个,
∴M点与椭圆短轴上的端点不重合,
∴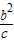 <b=
<b=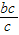 ,
,
∴b<c,b2+c2<2c2,
∵a2=b2+c2,
∴a2<2c2,∴a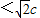 ,
,
∵0<e<1,
∴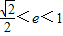 .
.
故答案为:(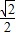 ,1).
,1).
点评:本题考果椭圆的离心率的取值范围的求法,解题时要认真审题,仔细解答,注意向量知识的合理运用.
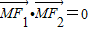 ,知,
,知,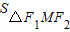 =b2,设M点纵坐标为h,则h=
=b2,设M点纵坐标为h,则h=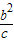 ,由椭圆上满足
,由椭圆上满足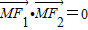 的M点有四个,得
的M点有四个,得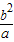 <
<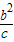 <b,由此能求出椭圆离心率的取值范围.
<b,由此能求出椭圆离心率的取值范围.解答:
 解:∵F1,F2是椭圆的两个焦点,在椭圆上满足
解:∵F1,F2是椭圆的两个焦点,在椭圆上满足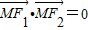 ,
,∴
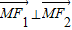 ,
,∴∠F1MF2=90°,
∴
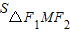 =b2,
=b2,设M点纵坐标为h,则
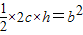 ,
,∴h=
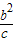 ,
,∵椭圆上满足
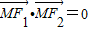 的M点有四个,
的M点有四个,∴M点与椭圆短轴上的端点不重合,
∴
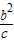 <b=
<b=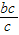 ,
,∴b<c,b2+c2<2c2,
∵a2=b2+c2,
∴a2<2c2,∴a
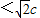 ,
,∵0<e<1,
∴
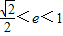 .
.故答案为:(
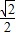 ,1).
,1).点评:本题考果椭圆的离心率的取值范围的求法,解题时要认真审题,仔细解答,注意向量知识的合理运用.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目