题目内容
【题目】设函数![]() 的定义域为
的定义域为![]() ,其中
,其中![]() .
.
(1)当![]() 时,写出函数
时,写出函数![]() 的单调区间(不要求证明);
的单调区间(不要求证明);
(2)若对于任意的![]() ,均有
,均有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;(2)当
;(2)当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
【解析】
试题分析:(1)对![]() 的取值范围分类讨论,去绝对值号后即可求解;(2)分析题意可知,问题等价于
的取值范围分类讨论,去绝对值号后即可求解;(2)分析题意可知,问题等价于![]() ,对
,对![]() 和
和![]() 的取值分类讨论,求得函数最值后即可求解.
的取值分类讨论,求得函数最值后即可求解.
试题解析:(1)当![]() 时:
时: ,∴
,∴![]() 单调递增区间是
单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;(2)当
;(2)当![]() 时:不等式
时:不等式![]() 成立;当
成立;当![]() 时:
时:![]() 等价于
等价于![]() ,设
,设![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
若![]() :
:![]() ,
,![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,
,
即![]() ,故
,故![]() ;若
;若![]() :
:![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,即
,即![]() ,故
,故![]() ;若
;若![]() :
:![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,![]() 上单调递减,
上单调递减,![]() 上单调递增,
上单调递增,![]() 上单调递增,∴
上单调递增,∴![]() ,而
,而![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]() ,故
,故![]() ;
;
若![]() :
:![]() ,
,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
∴![]() ,而
,而![]() ,
,![]() ,∴
,∴![]() ,
,![]() ;
;
若![]() :
:![]() ,
,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,![]() 上单调递减,在
上单调递减,在![]() 上单调递增,在
上单调递增,在![]() 上单调递增,
上单调递增,
∴![]() 且
且![]() ,而
,而![]()
![]() ,∴
,∴![]() 且
且![]() ,故当
,故当![]()
![]() 时,
时,
![]() ;当
;当![]() ,
,![]() ;
;
综上所述,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.

练习册系列答案
相关题目
【题目】在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;并估计,以运动为主的休闲方式的人的比例;
(2)能否在犯错误的概率不超过0.025的前提下,认为性别与休闲方式有关系?
附表:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2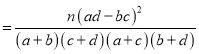 .
.