题目内容
取一根长度为3 m的绳子,拉直后在任意位置剪断,用随机模拟法估算剪得两段的长都不小于1 m的概率有多大?
思路分析:在任意位置剪断绳子,则剪断位置到一端点的距离取遍[0,3]内的任意实数,并且每一个实数被取到的可能性相等,因此在任意位置剪断绳子的所有结果(即基本事件)对应[0,3]上的均匀随机数,其中[1,2]上的均匀随机数就表示剪断位置与端点的距离在[1,2]内,也就是剪得两段的长都不小于1 m.这样取得的[1,2]内的随机数个数与[0,3]内的随机数个数之比就是事件A发生的频率.
解:设事件A“剪得两段的长都不小于1 m”.
S1 用计数器n记录做了多少次试验,用计数器m记录其中有多少次x出现在1—2之间(即剪得两段的长都不小于1 m).首先置n=0,m=0;
S2 用变换rand( )*3产生0—3之间的均匀随机数x;
S3 判断剪得的两段是否长度都大于1 m,即是否满足1<x<2.如果是,则计数器m的值加1,即m=m+1.如果不是,m的值保持不变;
S4 表示随机试验次数的计数器n的值加1,即n=n+1.如果还要继续试验,则返回步骤S2继续执行,否则,程序结束.
程序结束后事件A发生的频率![]() 作为事件A的概率的近似值.
作为事件A的概率的近似值.
温馨提示
用随机模拟法估算几何概率的关键是把事件A及基本事件空间对应的区域转化为随机数的范围.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
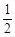 B.
B.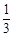 C.
C.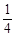 D.不确定
D.不确定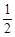 B.
B.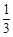 C.
C.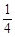 D.不确定
D.不确定