题目内容
在区间(0,2)内任取两数m,n(m≠n),则椭圆
+
=1的离心率大于
的概率是
.
| x2 |
| m2 |
| y2 |
| n2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
分析:由已知中在区间(0,2)内任取两个实数,我们易求出该基本事件对应的平面区域的大小,再求了满足条件椭圆
+
=1的离心率大于
对应的平面区域的面积大小,代入几何概型公式,即可得到答案.
| x2 |
| m2 |
| y2 |
| n2 |
| ||
| 2 |
解答: 解:区间(0,2)内任取两个实数计为(m,n),
解:区间(0,2)内任取两个实数计为(m,n),
则点对应的平面区域为下图所示的正方形,
当m>n时,椭圆
+
=1的离心率e=
>
,化简得,m>2n;
当M<n时,椭圆
+
=1的离心率e=
>
,化简得,n>2m;
故其中满足椭圆
+
=1的离心率大于
时,有m>2n或n>2m.
它表示的平面区域如下图中阴影部分所示:
其中正方形面积S=4,阴影部分面积S阴影=2×
×2×1=2.
∴所求的概率P=
=
故答案为:
.
 解:区间(0,2)内任取两个实数计为(m,n),
解:区间(0,2)内任取两个实数计为(m,n),则点对应的平面区域为下图所示的正方形,
当m>n时,椭圆
| x2 |
| m2 |
| y2 |
| n2 |
| ||
| m |
| ||
| 2 |
当M<n时,椭圆
| x2 |
| m2 |
| y2 |
| n2 |
| ||
| n |
| ||
| 2 |
故其中满足椭圆
| x2 |
| m2 |
| y2 |
| n2 |
| ||
| 2 |
它表示的平面区域如下图中阴影部分所示:
其中正方形面积S=4,阴影部分面积S阴影=2×
| 1 |
| 2 |
∴所求的概率P=
| S阴影 |
| S |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查的知识点是几何概型,其中计算出总的基本事件对应的几何图形的面积及满足条件的几何图形的面积是解答本题的关键.

练习册系列答案
相关题目
若在区间(-1,1)内任取实数a,在区间(0,1)内任取实数b,则直线ax-by=0与圆(x-1)2+(y-2)2=1相交的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
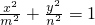 的离心率大于
的离心率大于 的概率是________.
的概率是________. 的离心率大于
的离心率大于 的概率是( ).
的概率是( ).