题目内容
10.在直线4x+3y-12=0上有一点P,它到点A(-1,-2)和点B(1,4)的距离相等,求点P的坐标.分析 根据题意,设出P的坐标,利用距离公式列方程求解即可.
解答 解:设直线4x+3y-12=0上的一点P为(a,4-$\frac{4}{3}$a),则PA=PB,
即$\sqrt{{(a+1)}^{2}{+(4-\frac{4}{3}a+2)}^{2}}$=$\sqrt{{(a-1)}^{2}{+(4-\frac{4}{3}a-4)}^{2}}$,
解得a=3;
所以点P(3,0).
点评 本题考查了两点间距离公式的应用问题,是基础题目.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
15.已知函数f(x)(x∈R),满足f(-x)=-f(x),f(3-x)=f(x),则f(435)=( )
| A. | 0 | B. | 3 | C. | -3 | D. | 不确定 |
2.方程x2-y2=-1表示( )
| A. | 焦点在x轴的双曲线 | B. | 圆 | ||
| C. | 两条直线 | D. | 焦点在y轴的双曲线 |
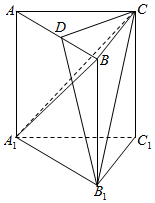 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点. 如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,AB=2AD=2,BD=$\sqrt{3}$,PD⊥平面ABCD.
如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,AB=2AD=2,BD=$\sqrt{3}$,PD⊥平面ABCD.