Question

已知数列{a_n}是正数组成的等差数列，S_n是其前n项的和，并且a₃=5,a₄S₂=28.

(1)求数列{a_n}的通项公式；

（2）求证：不等式(1+)(1+)…(1+)·对一切n∈N₊均成立.

Answer 1

思路分析：第（2）问中的不等式左侧，每个括号的规律是一致的，因此显得“多余”，所以可尝试变形，即把不等式两边同乘以，然后再证明.

(1)解：设数列{a_n}的公差为d，由已知，得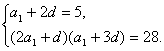

∴(10-3d)(5+d)=28,

∴3d²+5d-22=0,解之得d=2或d=.

∵数列{a_n}各项均为正，

∴d=2.∴a₁=1,

∴a_n=2n-1.

(2)证明：∵n∈N₊,

∴只需证明(1+)(1+)…(1+)

≥成立.

①当n=1时，左边=2，右边=2，

∴不等式成立.

②假设当n=k时，不等式成立，即

（1+）(1+)…(1+)≥.

那么当n=k+1时，

(1+)(1+)…(1+)(1+)

≥(1+)=

以下只需证明.

即只需证明2k+2≥.

∵(2k+2)²-()²=1＞0,

∴(1+)(1+)…(1+)

≥.

综上①②知，不等式对于n∈N⁺都成立.