题目内容
如图，棱柱ABCD-A1B1C1D1的底面ABCD为菱形，AC∩BD=O，侧棱AA1⊥BD，点F为DC1的中点，
(1)证明：OF∥平面BCC1B1；
(2)证明：平面DBC1⊥平面ACC1A1。
(1)证明：OF∥平面BCC1B1；
(2)证明：平面DBC1⊥平面ACC1A1。
证明：(1)∵四边形ABCD为菱形且AC∩BD=O，
∴O是BD的中点，
又点F为DC1的中点，则在△DBC1中，OF∥BC1，
∵OF
平面BCC1B1，B1C1
平面BCC1B1，
∴OF∥平面BCC1B1；
(2)∵四边形ABCD为菱形，
∴BD⊥AC，
又BD⊥AA1，AA1∩AC =A，且AA1、AC
平面ACC1A1，
∴BD⊥平面ACC1A1，
∵BD
平面DBC1，
∴平面DBC1⊥平面ACC1A1。
∴O是BD的中点，
又点F为DC1的中点，则在△DBC1中，OF∥BC1，
∵OF
平面BCC1B1，B1C1平面BCC1B1， ∴OF∥平面BCC1B1；
(2)∵四边形ABCD为菱形，
∴BD⊥AC，
又BD⊥AA1，AA1∩AC =A，且AA1、AC
平面ACC1A1，∴BD⊥平面ACC1A1，
∵BD
平面DBC1， ∴平面DBC1⊥平面ACC1A1。
练习册系列答案
相关题目
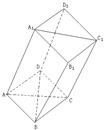如图，棱柱ABCD-A1B1C1D1的所有棱长都等于2，∠ABC和∠A1B1C1均为60°，平面AA1C1C⊥平面ABCD．
如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形，侧棱与底边长均为a，且∠A1AD=∠A1AB=60°．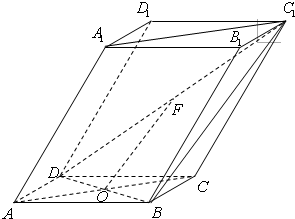
17、如图，棱柱ABCD-A1B1C1D1的底面ABCD为菱形，AC∩BD=O，侧棱AA1⊥BD，点F为DC1的中点．
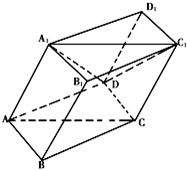如图，棱柱ABCD-A1B1C1D1的底面ABCD为菱形，平面AA1C1C⊥平面ABCD．?
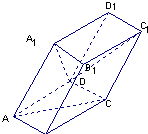如图，棱柱ABCD-A1B1C1D1的所有棱长都等于2，∠ABC=60°，平面AA1CC1⊥平面ABCD，∠A1AC=60°