题目内容
已知向量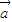 =(cos(-θ),sin(-θ)),
=(cos(-θ),sin(-θ)),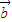 =
=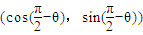 .
.(1)求证:
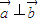 .
.(2)若存在不等于0的实数k和t,使
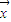 =
=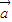 +(t2+3)
+(t2+3)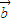 ,
, =(-k
=(-k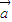 +t
+t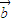 ),满足
),满足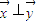 ,试求此时
,试求此时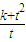 的最小值.
的最小值.
【答案】分析:(1)利用向量的数量积公式求出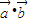 ,利用三角函数的诱导公式化简得数量积为0,利用向量垂直的充要条件得证.
,利用三角函数的诱导公式化简得数量积为0,利用向量垂直的充要条件得证.
(2)利用向量垂直的充要条件列出方程,利用向量的运算律化简方程,将方程中的k用t表示,代入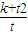 ,利用二次函数最值的求法求出最小值.
,利用二次函数最值的求法求出最小值.
解答:解:(1)证明∵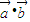 =cos(-θ)•cos(
=cos(-θ)•cos(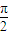 -θ)+sin(-θ)•sin
-θ)+sin(-θ)•sin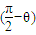 =sinθcosθ-sinθcosθ=0.
=sinθcosθ-sinθcosθ=0.
∴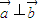 .
.
(2)解由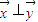 得
得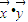 =0,
=0,
即[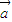 +(t2+3)
+(t2+3)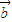 ]•(-k
]•(-k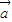 +t
+t )=0,
)=0,
∴-k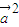 +(t3+3t)
+(t3+3t)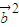 +[t2-k(t+3)]
+[t2-k(t+3)]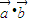 =0,
=0,
∴-k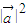 +(t3+3t)
+(t3+3t)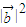 =0.
=0.
又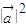 =1,
=1,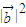 =1,
=1,
∴-k+t3+3t=0,
∴k=t3+3t.
∴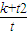 =
=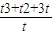 =t2+t+3=
=t2+t+3=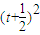 2+
2+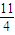 .
.
故当t=- 时,
时,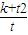 有最小值
有最小值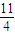 .
.
点评:本题考查向量垂直的充要条件、向量的运算律、二次函数最值的求法.
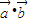 ,利用三角函数的诱导公式化简得数量积为0,利用向量垂直的充要条件得证.
,利用三角函数的诱导公式化简得数量积为0,利用向量垂直的充要条件得证.(2)利用向量垂直的充要条件列出方程,利用向量的运算律化简方程,将方程中的k用t表示,代入
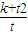 ,利用二次函数最值的求法求出最小值.
,利用二次函数最值的求法求出最小值.解答:解:(1)证明∵
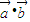 =cos(-θ)•cos(
=cos(-θ)•cos(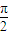 -θ)+sin(-θ)•sin
-θ)+sin(-θ)•sin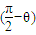 =sinθcosθ-sinθcosθ=0.
=sinθcosθ-sinθcosθ=0.∴
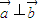 .
.(2)解由
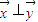 得
得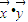 =0,
=0,即[
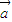 +(t2+3)
+(t2+3)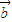 ]•(-k
]•(-k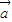 +t
+t )=0,
)=0,∴-k
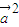 +(t3+3t)
+(t3+3t)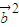 +[t2-k(t+3)]
+[t2-k(t+3)]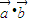 =0,
=0,∴-k
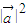 +(t3+3t)
+(t3+3t)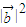 =0.
=0.又
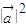 =1,
=1,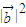 =1,
=1,∴-k+t3+3t=0,
∴k=t3+3t.
∴
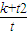 =
=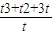 =t2+t+3=
=t2+t+3=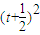 2+
2+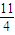 .
.故当t=-
 时,
时,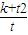 有最小值
有最小值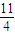 .
.点评:本题考查向量垂直的充要条件、向量的运算律、二次函数最值的求法.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |