题目内容
如图，在正六边形ABCDEF中，已知| AC |
| AD |
| AE |
分析：据相等向量的定义及向量的减法法则得
，
，再据向量的加法法则求
．
| OE |
| AO |
| AE |
解答：解：连接BE、CF，它们交于点O，则
=d-c，
由正六边形的性质得
=
=
=d-c，
又
=
d，∴
=
+
=
d+(d-c)=
d-c．
故答案为
d-c
| CD |
由正六边形的性质得
| OE |
| BO |
| CD |
又
| AO |
| 1 |
| 2 |
| AE |
| AO |
| OE |
| 1 |
| 2 |
| 3 |
| 2 |
故答案为
| 3 |
| 2 |
点评：本题考查向量相等的概念、向量加减法的三角形及平行四边形法则、向量共线的充要条件．
练习册系列答案
相关题目
1、如图，在直角坐标平面内有一个边长为a，中心在原点O的正六边形ABCDEF，AB∥Ox．直线L：y=kx+t（k为常数）与正六边形交于M、N两点，记△OMN的面积为S，则函数S=f（t）的奇偶性为
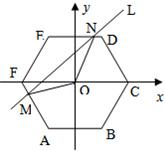如图，在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF，AB∥Ox．直线L：y=kx+t（k为常数）与正六边形交于M、N两点，记△OMN的面积为S，则函数S=f（t）的奇偶性为（ ）| A、偶函数 | B、奇函数 | C、不是奇函数，也不是偶函数 | D、奇偶性与k有关 |
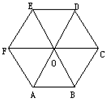如图，在正六边形ABCDEF中，点O为其中心，则下列判断错误的是（ ）