题目内容

已知正三角形ABC的边长为a,在平面上求一点P,使|PA|2+|PB|2+|PC|2最小,并求出此最小值.

解:如图,以BC所在直线为x轴,BC的垂直平分线为y轴建立直角坐标系,则A(0, a),B(-,0),C(,0).?

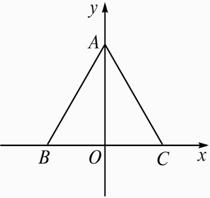
设P(x,y),则|PA|2+|PB|2+|PC|2

=x2+(y- a)2+(x+)2+y2+(x-)2+y2?

=3x2+3y2-ay+=3x2+3(y-a)2+a2≥a2,

当且仅当x=0,y=a时,等号成立,?

∴所求最小值为a2,此时P点坐标为P(0,a),是正三角形ABC的中心.

练习册系列答案
相关题目
已知正三角形ABC的边长为a，那么三角形ABC根据斜二测画法得到的平面直观图三角形A′B′C′的面积为（　　）
A、
3
4
a2
B、
3
8
a2
C、
6
8
a2
D、
6
16
a2
已知正三角形ABC的边长为a，求△ABC的直观图△A′B′C′的面积．
已知正三角形ABC的边长为1，且
BA
=
a
，
AC
=
b
，则|
a
-
b
|=（　　）
A、
3
B、3
C、
2
D、1
（2012•黑龙江）已知正三角形ABC的顶点A（1，1），B（1，3），顶点C在第一象限，若点（x，y）在△ABC内部，则z=-x+y的取值范围是（　　）
如图，已知正三角形ABC的边长为2，点D为边AC的中点，点E为边AB上离点A较近的三等分点，则
BD
•
CE
=
-1
-1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网