题目内容
19.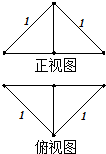 把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的正视图与俯视图如图所示,则三棱锥C-ABD的体积为$\frac{\sqrt{2}}{12}$,表面积为1+$\frac{\sqrt{3}}{2}$.
把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的正视图与俯视图如图所示,则三棱锥C-ABD的体积为$\frac{\sqrt{2}}{12}$,表面积为1+$\frac{\sqrt{3}}{2}$.
分析 根据几何体的三视图,得出该几何体是底面为等腰直角三角形,且侧面BCD⊥底面ABD,
结合图中数据求出它的体积与表面积.
解答 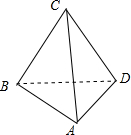 解:根据几何体的三视图,得;
解:根据几何体的三视图,得;
该几何体是底面为等腰直角三角形的三棱锥;
如图所示,
且侧面BCD⊥底面ABD,;
所以,该三棱锥的体积为
V三棱锥=$\frac{1}{3}$•$\frac{1}{2}$•12•$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{12}$;
又AC=$\sqrt{{(\frac{\sqrt{2}}{2})}^{2}{+(\frac{\sqrt{2}}{2})}^{2}}$=1,
所以,△ABC与△ADC是边长为1的等边三角形,
所以,该三棱锥的表面积为
S表面积=2×$\frac{1}{2}$×12+2×$\frac{1}{2}$×12×sin$\frac{π}{3}$=1+$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{{\sqrt{2}}}{12}$、$1+\frac{{\sqrt{3}}}{2}$.
点评 本题考查了利用空间几何体的三视图求几何体的体积与表面积的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.设z是复数,则下列命题中的真命题是( )
| A. | 若z2<0,则|z|=-z+i | B. | 若z2<0,则$\frac{z}{1+i}$的共轭虚数$\frac{z}{i-1}$ | ||
| C. | 若z是虚数,则z2≥0 | D. | 若z2≥0,则$\frac{z}{1+i}$的共轭虚数$\frac{z}{i-1}$ |
9.若$sin(\frac{π}{3}-α)=\frac{1}{4}$,则$cos(\frac{π}{6}+α)$=( )
| A. | $-\frac{7}{8}$ | B. | $-\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{7}{8}$ |
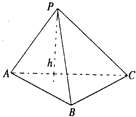 在Rt△ABC中,两直角边分别为a,b,设h为斜边上的高,则$\frac{1}{h^2}$=$\frac{1}{a^2}$+$\frac{1}{b^2}$,类比此性质,如图,在四面体P-ABC 中,若PA,PB,PC两两垂直,且长度分别为a,b,c,设棱锥底面ABC上的高为h,则得到的正确结论为$\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$.
在Rt△ABC中,两直角边分别为a,b,设h为斜边上的高,则$\frac{1}{h^2}$=$\frac{1}{a^2}$+$\frac{1}{b^2}$,类比此性质,如图,在四面体P-ABC 中,若PA,PB,PC两两垂直,且长度分别为a,b,c,设棱锥底面ABC上的高为h,则得到的正确结论为$\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$.