题目内容
已知在直角坐标系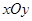 中,曲线
中,曲线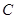 的参数方程为:
的参数方程为: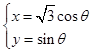 (
(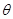 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系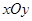 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线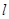 的极坐标方程为:
的极坐标方程为: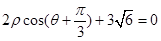 .
.
(Ⅰ)写出曲线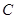 和直线
和直线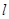 在直角坐标系下的方程;
在直角坐标系下的方程;
(II)设点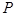 是曲线
是曲线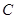 上的一个动点,求它到直线
上的一个动点,求它到直线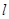 的距离的最小值.
的距离的最小值.
(Ⅰ) ;(II)
;(II) .
.
解析试题分析:(Ⅰ)利用转化公式参数方程、极坐标方程为直角坐标方程;(II)利用点到直线距离公式得点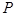 它到直线
它到直线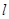 的距离的函数关系式,最后利用函数求最值.
的距离的函数关系式,最后利用函数求最值.
试题解析:(Ⅰ) ,
,
所以曲线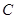 在直角坐标系下的标准方程是
在直角坐标系下的标准方程是

又
故直线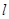 在直角坐标系下的标准方程是
在直角坐标系下的标准方程是

(II)设 ,于是点
,于是点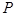 到直线
到直线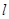 的距离为
的距离为
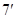


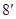

当 即
即 时取等号,此时
时取等号,此时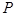 为
为
所以点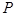 到直线
到直线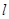 的距离的最小值为
的距离的最小值为

考点:考查选坐标系与参数方程.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
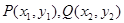 是抛物线
是抛物线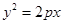
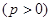 上相异两点,
上相异两点,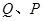 到y轴的距离的积为
到y轴的距离的积为 且
且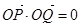 .
.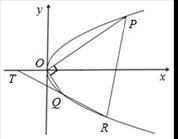
 轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值.
轴交点为T,且Q为线段RT的中点,试求弦PR长度的最小值. 在
在 轴右边,
轴右边,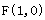 的距离减去它到
的距离减去它到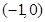 的直线
的直线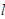 与曲线C有两个交点
与曲线C有两个交点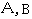 ,且
,且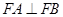 ,求直线
,求直线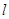 的斜率.
的斜率.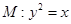 与曲线
与曲线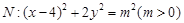 相交于
相交于 、
、 、
、 、
、 四个点.
四个点.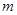 的取值范围;
的取值范围; 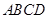 的面积的最大值及此时对角线
的面积的最大值及此时对角线 与
与 的交点坐标.
的交点坐标.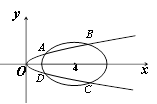
 的参数方程为
的参数方程为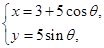
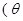 是参数
是参数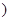 ,
,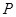 是曲线
是曲线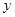 轴正半轴的交点.以坐标原点
轴正半轴的交点.以坐标原点 为极点,
为极点,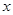 轴正半轴为极轴建立极坐标系,求经过点
轴正半轴为极轴建立极坐标系,求经过点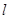 的极坐标方程.
的极坐标方程.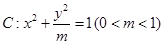 的左顶点为
的左顶点为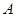 ,
,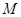 是椭圆
是椭圆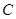 上异于点
上异于点 与点
与点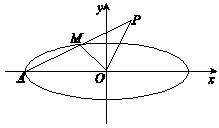
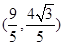 ,求
,求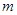 的值;
的值;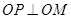 ,求
,求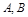 分别是椭圆
分别是椭圆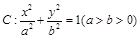 的左、右顶点,点
的左、右顶点,点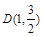 在椭圆
在椭圆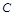 上,且直线
上,且直线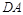 与直线
与直线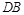 的斜率之积为
的斜率之积为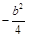 .
. 是椭圆
是椭圆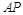 与
与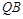 交于点
交于点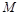 ,直线
,直线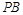 与
与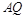 交于点
交于点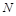 .① 求证:
.① 求证: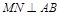 ;② 若弦
;② 若弦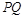 过椭圆的右焦点
过椭圆的右焦点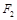 ,求直线
,求直线 的方程.
的方程.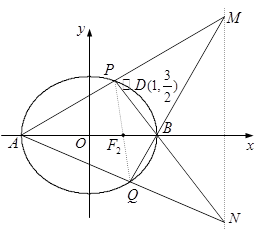
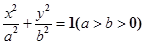 的两个顶点,
的两个顶点, 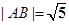 ,直线AB的斜率为
,直线AB的斜率为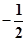 .求椭圆的方程;(2)设直线
.求椭圆的方程;(2)设直线 平行于AB,与x,y轴分别交于点M、N,与椭圆相交于C、D,
平行于AB,与x,y轴分别交于点M、N,与椭圆相交于C、D,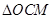 的面积等于
的面积等于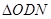 的面积.
的面积.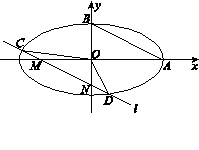
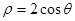 ,曲线C2的参数方程为
,曲线C2的参数方程为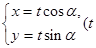 为参数)。
为参数)。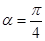 时,求曲线Cl与C2公共点的直角坐标;
时,求曲线Cl与C2公共点的直角坐标; 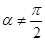 ,当
,当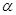 变化时,设曲线C1与C2的公共点为A,B,试求AB中点M轨迹的极坐标方程,并指出它表示什么曲线.
变化时,设曲线C1与C2的公共点为A,B,试求AB中点M轨迹的极坐标方程,并指出它表示什么曲线.