题目内容
已知圆F1:(x+2)2+y2=1,圆F2:(x-2)2+y2=4,动圆与圆F1内切且与圆F2外切,则动圆圆心的轨迹方程是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
分析:据两圆外切和内切的判定,圆心距与两圆半径和差的关系,设出动圆半径为r,消去r,根据圆锥曲线的定义,即可求得动圆圆心M的轨迹,进而可求其方程.
解答:解:设动圆圆心M(x,y),半径为r,
∵圆M与圆F1:(x+2)2+y2=1内切且与圆F2:(x-2)2+y2=4外切,
∴|MF1|=r-1,|MF2|=r+2,
∴|MF2|-|MF1|=3<4,
∴点M的轨迹是以点F1,F2为焦点的双曲线的左支,
∴动圆圆心M的轨迹方程是
-
=1(x≤-
),
故选D.
∵圆M与圆F1:(x+2)2+y2=1内切且与圆F2:(x-2)2+y2=4外切,
∴|MF1|=r-1,|MF2|=r+2,
∴|MF2|-|MF1|=3<4,
∴点M的轨迹是以点F1,F2为焦点的双曲线的左支,
∴动圆圆心M的轨迹方程是
| 4x2 |
| 9 |
| 4y2 |
| 7 |
| 3 |
| 2 |
故选D.
点评:考查两圆的位置关系及判定方法和双曲线的定义和标准方程,特别注意是轨迹是双曲线的一支还是双支,这是学生在解题中最易忽视的地方,属中档题.

练习册系列答案
相关题目
 已知圆F1:(x+1)2+y2=16,定点F2(1,0),动圆过点F2,且与圆F1相内切.
已知圆F1:(x+1)2+y2=16,定点F2(1,0),动圆过点F2,且与圆F1相内切.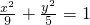
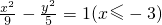
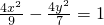
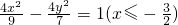
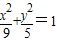
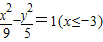
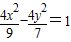
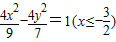
 已知圆F1:(x+1)2+y2=16,定点F2(1,0),动圆过点F2,且与圆F1相内切.
已知圆F1:(x+1)2+y2=16,定点F2(1,0),动圆过点F2,且与圆F1相内切.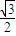 ,求直线l的方程.
,求直线l的方程.