题目内容
如图,在三棱锥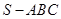 中,平面
中,平面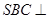 平面
平面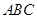 ,
,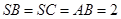 ,
,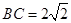 ,
,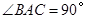 ,
,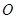 为
为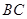 中点.(Ⅰ)求点B到平面
中点.(Ⅰ)求点B到平面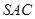 的距离;(Ⅱ)求二面角
的距离;(Ⅱ)求二面角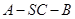 的余弦值.
的余弦值.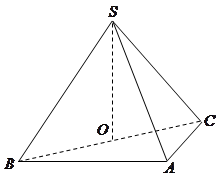
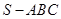 中,平面
中,平面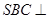 平面
平面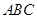 ,
,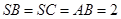 ,
,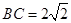 ,
,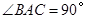 ,
,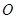 为
为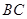 中点.(Ⅰ)求点B到平面
中点.(Ⅰ)求点B到平面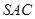 的距离;(Ⅱ)求二面角
的距离;(Ⅱ)求二面角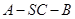 的余弦值.
的余弦值.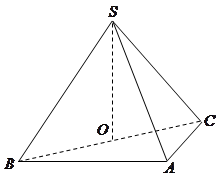
(Ⅰ) (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
第一问中利用因为 ,
,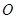 为
为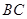 中点,所以
中点,所以
而平面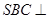 平面
平面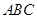 ,所以
,所以 平面
平面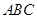 ,再由题设条件知道可以分别以
,再由题设条件知道可以分别以 、
、 、
、 为
为 ,
, ,
,  轴建立直角坐标系得
轴建立直角坐标系得 ,
, ,
, ,
, ,
, ,
, ,
,
故平面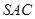 的法向量
的法向量 而
而 ,故点B到平面
,故点B到平面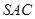 的距离
的距离
第二问中,由已知得平面 的法向量
的法向量 ,平面
,平面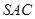 的法向量
的法向量
故二面角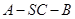 的余弦值等于
的余弦值等于
解:(Ⅰ)因为 ,
,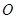 为
为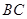 中点,所以
中点,所以
而平面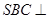 平面
平面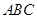 ,所以
,所以 平面
平面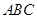 ,
,
再由题设条件知道可以分别以 、
、 、
、 为
为 ,
, ,
,  轴建立直角坐标系,得
轴建立直角坐标系,得 ,
, ,
, ,
, ,
,
 ,
, ,故平面
,故平面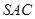 的法向量
的法向量
而 ,故点B到平面
,故点B到平面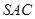 的距离
的距离
(Ⅱ)由已知得平面 的法向量
的法向量 ,平面
,平面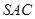 的法向量
的法向量
故二面角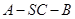 的余弦值等于
的余弦值等于
 ,
,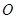 为
为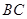 中点,所以
中点,所以
而平面
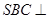 平面
平面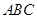 ,所以
,所以 平面
平面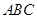 ,再由题设条件知道可以分别以
,再由题设条件知道可以分别以 、
、 、
、 为
为 ,
, ,
,  轴建立直角坐标系得
轴建立直角坐标系得 ,
, ,
, ,
, ,
, ,
, ,
,故平面
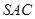 的法向量
的法向量 而
而 ,故点B到平面
,故点B到平面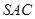 的距离
的距离
第二问中,由已知得平面
 的法向量
的法向量 ,平面
,平面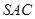 的法向量
的法向量
故二面角
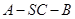 的余弦值等于
的余弦值等于
解:(Ⅰ)因为
 ,
,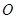 为
为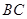 中点,所以
中点,所以
而平面
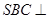 平面
平面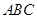 ,所以
,所以 平面
平面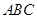 ,
,再由题设条件知道可以分别以
 、
、 、
、 为
为 ,
, ,
,  轴建立直角坐标系,得
轴建立直角坐标系,得 ,
, ,
, ,
, ,
, ,
, ,故平面
,故平面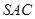 的法向量
的法向量
而
 ,故点B到平面
,故点B到平面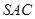 的距离
的距离
(Ⅱ)由已知得平面
 的法向量
的法向量 ,平面
,平面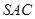 的法向量
的法向量
故二面角
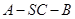 的余弦值等于
的余弦值等于

练习册系列答案
相关题目
 与平面
与平面 所成的角为30°,
所成的角为30°, 为空间一定点,过
为空间一定点,过 ,则这样的直线
,则这样的直线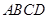 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直,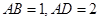 ,
,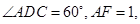
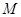 是线段
是线段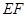 的中点.
的中点.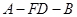 的正弦值;
的正弦值;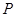 为一动点,若点
为一动点,若点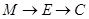 的路线运动到点
的路线运动到点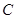 ,求这一过程中形成的三棱锥
,求这一过程中形成的三棱锥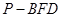 的体积的最小值.
的体积的最小值.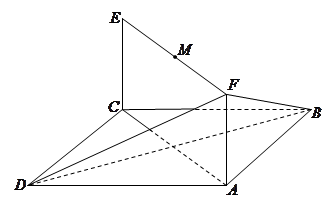
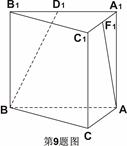
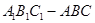 是直三棱柱,
是直三棱柱,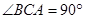 ,点
,点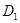 、
、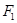 分别是
分别是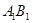 ,
,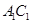 的中点,若
的中点,若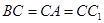 ,则
,则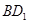 与
与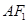 所成角的余弦值是( )
所成角的余弦值是( )



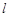 与这三条直线所成的角均为
与这三条直线所成的角均为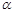 ,则
,则 .
.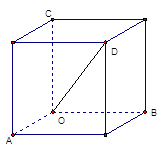
 中,
中,
 ,
, .
. 中,
中, 与平面
与平面 所成角的正弦值为( )
所成角的正弦值为( )



