题目内容
若实数a、b满足a+b=2则2a+2b的最小值是
- A.8
- B.4
- C.2
- D.2
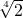
B
分析：根据基本不等式和指数运算2a+2b≥2
=2 
=6，要检验等号何时取得．
解答：∵a+b=2
∴2a+2b≥2=2 =4
当且仅当a=b=1时等号成立
故选B．
点评：本题主要考查基本不等式的应用，应用基本不等式时要注意“一正、二定、三相等”，为要满足的条件．
分析：根据基本不等式和指数运算2a+2b≥2
=2 =6，要检验等号何时取得．解答：∵a+b=2
∴2a+2b≥2
=2 =4当且仅当a=b=1时等号成立
故选B．
点评：本题主要考查基本不等式的应用，应用基本不等式时要注意“一正、二定、三相等”，为要满足的条件．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若实数a，b满足a≥0，b≥0，且ab=0，则称a与b互补，记φ（a，b）=
-a-b那么φ（a，b）=0是a与b互补的（ ）
| a2+b2 |
| A、必要不充分条件 |
| B、充分不必要的条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
﹣a﹣b那么φ(a，b）=0是a与b互补的 
，那么φ（a，b）=0是a与b互补的