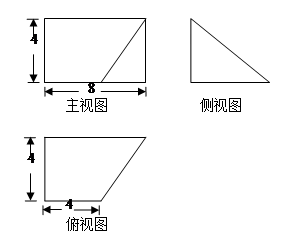
题目内容
如图, 为圆
为圆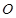 的直径,点
的直径,点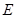 、
、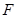 在圆
在圆 上,矩形
上,矩形 所在的平面和圆
所在的平面和圆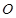 所在的平面互相垂直,且
所在的平面互相垂直,且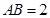 ,
, .
.
(Ⅰ)求证: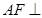 平面
平面 ;
;
(Ⅱ)求三棱锥 的体积.
的体积.
(Ⅰ)利用线线垂直证明线面垂直(Ⅱ)
解析试题分析:(Ⅰ)平面
 平面
平面 ,
, ,
,
平面
 平面
平面 ,
, 平面
平面 ,
,
∵AF在平面 内,∴
内,∴ , 3分
, 3分
又 为圆
为圆 的直径,∴
的直径,∴ ,
,
∴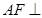 平面
平面 . 6分
. 6分
(Ⅱ)由(1)知 即
即 ,
,
∴三棱锥 的高是
的高是 ,
,
∴ , 8分
, 8分
连结 、
、 ,可知
,可知
∴ 为正三角形,∴正
为正三角形,∴正 的高是
的高是 , 10分
, 10分
∴ , 12分
, 12分
考点:本题考查了空间中的线面关系
点评:此类问题常考查空间中平行关系与垂直关系的证明以及几何体体积的计算,这是高考的重点内容.证明的关键是熟练掌握并灵活运用相关的判定定理与性质定理

练习册系列答案
相关题目
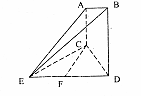
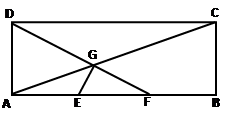
 是正三角形,AB
是正三角形,AB 平面BCD,
平面BCD, ,E为BC的中点,F在棱AC上,且
,E为BC的中点,F在棱AC上,且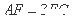

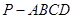 中,底面
中,底面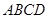 是矩形,
是矩形,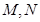 分别为
分别为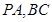 的中点,
的中点,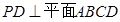 ,且
,且
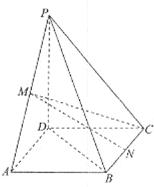
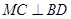 ;
; 的余弦值。
的余弦值。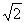 .
.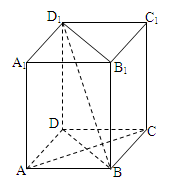
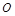 为正方形
为正方形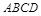 的中心,四边形
的中心,四边形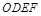 是平行四边形,且平面
是平行四边形,且平面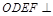 平面
平面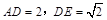 .
.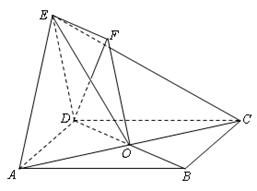
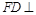 平面
平面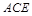 .
.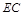 上是否存在一点
上是否存在一点 ,使
,使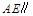 平面
平面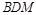 ?若存在,求
?若存在,求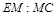 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.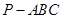 中,
中,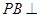 底面
底面 于
于 ,
, ,
, ,点
,点 是
是 的中点.
的中点.
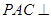 平面
平面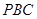 ;
;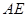 与
与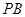 所成的角为
所成的角为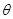 ,且
,且 ,
,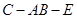 的大小.
的大小.  ; (2)求证:
; (2)求证: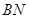
 ;
; 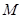 为
为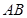 中点,在
中点,在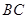 边上找一点
边上找一点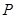 ,使
,使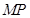
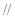 平面
平面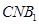 ,并求
,并求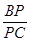 的值.
的值.