题目内容
若函数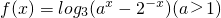 在[1,+∞)上大于1恒成立,则a的取值范围是
在[1,+∞)上大于1恒成立,则a的取值范围是
- A.

- B.
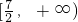
- C.(3,+∞)
- D.[3,+∞)
A
分析:f(x)>1在区间[1,+∞)上恒成立等价于ax-2 -x>3在区间[1,+∞)上恒成立,分离参数得ax>3+2 -x,构造函数,画出图象,建立a的不等关系,即可得到a的取值范围.
解答: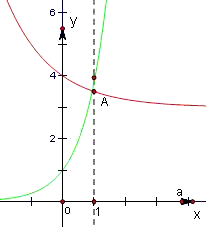 解:f(x)>1在区间[1,+∞)上恒成立等价于ax-2 -x>3在区间[1,+∞)上恒成立
解:f(x)>1在区间[1,+∞)上恒成立等价于ax-2 -x>3在区间[1,+∞)上恒成立
得ax>3+2 -x令h(x)=3+2 -x,g(x)=ax
分别画出函数h(x)和g(x)的图象,
由图象,得当x=1时,g(1)的值必须大于h(1)即可.
所以a>3+ =
= ,
,
因此a的取值范围是 .
.
故选A.
点评:本题考查对数函数的图象与性质,考查恒成立问题,解题的关键是分离参数,数形结合,属于中档题.
分析:f(x)>1在区间[1,+∞)上恒成立等价于ax-2 -x>3在区间[1,+∞)上恒成立,分离参数得ax>3+2 -x,构造函数,画出图象,建立a的不等关系,即可得到a的取值范围.
解答:
 解:f(x)>1在区间[1,+∞)上恒成立等价于ax-2 -x>3在区间[1,+∞)上恒成立
解:f(x)>1在区间[1,+∞)上恒成立等价于ax-2 -x>3在区间[1,+∞)上恒成立得ax>3+2 -x令h(x)=3+2 -x,g(x)=ax
分别画出函数h(x)和g(x)的图象,
由图象,得当x=1时,g(1)的值必须大于h(1)即可.
所以a>3+
 =
= ,
,因此a的取值范围是
 .
.故选A.
点评:本题考查对数函数的图象与性质,考查恒成立问题,解题的关键是分离参数,数形结合,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在[1,3]上是减函数,求实数a的取值范围.
在[1,3]上是减函数,求实数a的取值范围. 在[1,+∞)上是增函数,不等式
在[1,+∞)上是增函数,不等式 在[1,+∞)上恒成立,求实数a的取值范围.
在[1,+∞)上恒成立,求实数a的取值范围. .
. 在点(1,
在点(1, )处的切线方程;
)处的切线方程; 在[1,2]上是减函数,求实数a的取值范围;
在[1,2]上是减函数,求实数a的取值范围; 是否存在实数a,当
是否存在实数a,当 是自然对数的底)时,函数
是自然对数的底)时,函数 的最小值是3,若存在,求出a的值;若不存在,说明理由.
的最小值是3,若存在,求出a的值;若不存在,说明理由. 的距离小1.
的距离小1. 当△AOB的面积为
当△AOB的面积为 时(O为坐标原点),求的值.
时(O为坐标原点),求的值. 在[1,3]上是减函数,求实数a的取值范围.
在[1,3]上是减函数,求实数a的取值范围.