题目内容
(本小题满分12分)已知等差数列{an}的首项为1,前n项和为 ,且S1,S2,S4成等比数列.
,且S1,S2,S4成等比数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)记 为数列
为数列 的前
的前 项和,是否存在正整数n,使得
项和,是否存在正整数n,使得 ?若存在,求
?若存在,求 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
(Ⅰ) 或
或  ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
试题分析:(Ⅰ)设数列 的公差为
的公差为 ,由题设列方程求解
,由题设列方程求解 的值,从而得到数列
的值,从而得到数列 的通项公式;
的通项公式;
(Ⅱ)当 时,
时, ,此时不存在正整数n,使得
,此时不存在正整数n,使得 ;
;
当 时,根据
时,根据 =
=
 ,利用裂项法化简
,利用裂项法化简 的表达式,通过解不等式
的表达式,通过解不等式 求解.
求解.
试题解析:【解析】
(Ⅰ)设数列 的公差为
的公差为 ,依题意,1,
,依题意,1, ,
, 成等比数列,
成等比数列,
所以 ,即
,即 ,所以
,所以 或
或 .
.
因此,当 时,
时, ;当
;当 时,
时, . (6分)
. (6分)
(Ⅱ)当 时,
时, ,此时不存在正整数n,使得
,此时不存在正整数n,使得 ;
;
当 时,
时,

 .
.
由 ,得
,得 ,解得
,解得 .
.
故 的最大值为1006. (12分)
的最大值为1006. (12分)
考点:1、等差数列;2、裂项法求数列的前 项和.
项和.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 异面,
异面, 异面,则
异面,则 异面;
异面; ,则
,则 所成的角相等;
所成的角相等; ,
, ,则
,则 .
. 的平均数是5,标准差是
的平均数是5,标准差是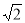 ,则
,则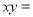 ( )
( )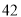 B.
B.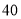 C.
C. D.
D.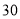
 在区间
在区间 上单调递增,且在这个区间上的最大值是
上单调递增,且在这个区间上的最大值是 ,那么
,那么
 B.
B. C.2 D.4
C.2 D.4 ,集合
,集合 ,
, ,则
,则
 B.
B.
 D.
D.
 的直线
的直线 与双曲线
与双曲线 交于不同的两点P、Q,若点P、Q在
交于不同的两点P、Q,若点P、Q在 轴上的射影恰好为双曲线的两个焦点,则该双曲线的离心率是 .
轴上的射影恰好为双曲线的两个焦点,则该双曲线的离心率是 .
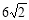 和40
和40 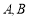 两点的坐标分别为
两点的坐标分别为 ,
, ,
,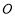 为坐标原点,动点
为坐标原点,动点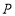 满足
满足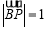 ,则
,则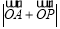 的最小值是( ).
的最小值是( ).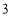 B.
B.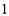 C.
C. D.
D.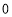
 =
= ,则
,则 = .
= .