题目内容
已知函数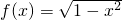 ,若直线y=2x+m与函数图象始终相交,则实数m的取值范围________.
,若直线y=2x+m与函数图象始终相交,则实数m的取值范围________.
[-2, ]
]
分析:由题意可得,函数的图象表示一个半圆,直线y=2x+m与函数图象始终相切时,由1=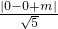 求得 m的值.当直线y=2x+m过点A(1,0)时,求得m的值,数形结合可得
求得 m的值.当直线y=2x+m过点A(1,0)时,求得m的值,数形结合可得
实数m的取值范围.
解答:由函数y=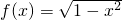 ,可得 x2+y2=1 (y≥0),表示一个以原点O为圆心,半径等于1的位于x轴及x轴上方的半圆,如图所示:
,可得 x2+y2=1 (y≥0),表示一个以原点O为圆心,半径等于1的位于x轴及x轴上方的半圆,如图所示:
由于直线y=2x+m与函数图象始终相切,由1=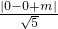 求得 m=
求得 m= ,或 m=-
,或 m=- (舍去).
(舍去).
当直线y=2x+m过点A(1,0)时,有0=2+m,m=-2.
数形结合可得实数m的取值范围是[-2, ],
],
故答案为[-2, ].
].
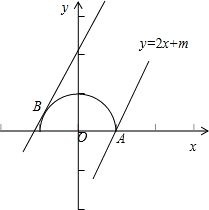
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式,体现了数形结合的数学思想,属于基础题.
 ]
]分析:由题意可得,函数的图象表示一个半圆,直线y=2x+m与函数图象始终相切时,由1=
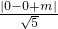 求得 m的值.当直线y=2x+m过点A(1,0)时,求得m的值,数形结合可得
求得 m的值.当直线y=2x+m过点A(1,0)时,求得m的值,数形结合可得实数m的取值范围.
解答:由函数y=
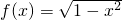 ,可得 x2+y2=1 (y≥0),表示一个以原点O为圆心,半径等于1的位于x轴及x轴上方的半圆,如图所示:
,可得 x2+y2=1 (y≥0),表示一个以原点O为圆心,半径等于1的位于x轴及x轴上方的半圆,如图所示:由于直线y=2x+m与函数图象始终相切,由1=
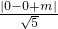 求得 m=
求得 m= ,或 m=-
,或 m=- (舍去).
(舍去).当直线y=2x+m过点A(1,0)时,有0=2+m,m=-2.
数形结合可得实数m的取值范围是[-2,
 ],
],故答案为[-2,
 ].
].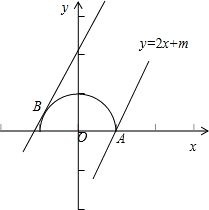
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式,体现了数形结合的数学思想,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
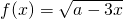 的反函数为y=f-1(x)
的反函数为y=f-1(x)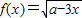 的反函数为y=f-1(x)
的反函数为y=f-1(x)