题目内容
在△ABC中, 角A、B、C对边a、b、c,若(a2+c2-b2)tanB= ac,则角B=
ac,则角B=
A. B.
B. C.
C. 或
或 D.
D. 或
或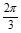
D
解析试题分析:因为(a2+c2-b2)tanB= ac,所以
ac,所以 ,又因为
,又因为 ,所以B=
,所以B= 或
或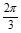
考点:本题主要考查余弦定理。
点评:本题难度适中,又能突出基础,很难得。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的三边之比为3:5:7,求这个三角形的最大角为( )
的三边之比为3:5:7,求这个三角形的最大角为( )
A. | B. | C. | D. |
.在 中,已知
中,已知 ,则角
,则角 为 ( )
为 ( )
A. | B. | C. | D. 或 或 |
在△ABC中,a=
 ,b=
,b= ,B=45°,则A等于( )
,B=45°,则A等于( )
| A.30° | B.60° | C.60°或120° | D.30°或150° |
在△ 中,内角
中,内角 的对边分别为
的对边分别为 。若
。若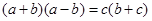 ,则
,则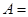
A.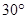 | B.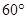 | C.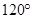 | D.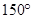 |
某人要制作一个三角形,要求它的三条高的长度分别为 则此人能( )
则此人能( )
| A.不能作出这样的三角形. | B.作出一个锐角三角形. |
| C.作出一个直角三角形. | D.作出一个钝角三角形. |
 中,
中, ,BC=3,则
,BC=3,则 的周长为( )
的周长为( )
A. | B. |
C. | D. |
 中,
中, ,则A等于 ( )
,则A等于 ( )
 与两灯塔A、B的距离分别为300米和500米,测得灯塔A在观察站C北偏东30
与两灯塔A、B的距离分别为300米和500米,测得灯塔A在观察站C北偏东30 ,灯塔B在观察站C正西方向,则两灯塔A、B间的距离为
,灯塔B在观察站C正西方向,则两灯塔A、B间的距离为