Question

等边三角形ABC与正方形ABDE有一公共边AB，二面角C-AB-D为直二面角，M，N分别是AC，BC的中点，则EM，AN所成角的余弦值为________．

Answer 1

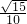
分析：取DE的中点F，由三角形ABC为等边三角形，四边形ABDE为正方形，由M，N分别是AC，BC的中点，我们易证得ME∥NF，则∠ANF或其补角为异面直线AN，EM所成的角，解△ANF即可得到EM，AN所成角的余弦值．
解答：设DE的中点为F，可证四边形MNFE为平行四边形，
故ME∥NF，
∴∠ANF或其补角为异面直线AN，EM所成的角，
在△ANF中，运用余弦定理求得．
故答案为：
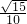
点评：本题考查的知识点是与二面角有关的立体几何综合题，空间异面直线之间的夹角，其中通过平移法求两条异面直线的夹角是本题的关键．