题目内容
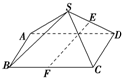如图所示，S为矩形ABCD所在平面外一点，E、F分别是SD、BC上的点，且SE：ED=BF：FC，求证：EF∥平面SAB．分析：在SC上取一点H，使SH：HC=SE：ED，则EH∥DC，EH∥AB，可得EH∥平面SAB，再证明HF∥平面SAB，利用面面平行的判定可得平面EHF∥平面SAB，从而可得EF∥平面SAB．
解答：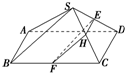
证明：如图所示，在SC上取一点H，使SH：HC=SE：ED，则EH∥DC．
∵DC∥AB，∴EH∥AB，
∵EH?平面SAB，AB?平面SAB
∴EH∥平面SAB
∵SE：ED=BF：FC，EH∥DC
∴SH：HC=BF：FC，
∴HF∥BS
∵HF?平面SAB，BS?平面SAB
∴HF∥平面SAB
∵FH∩HE=H．
∴平面EHF∥平面SAB．
∵EF?平面EHF，
∴EF∥平面SAB．
证明：如图所示，在SC上取一点H，使SH：HC=SE：ED，则EH∥DC．∵DC∥AB，∴EH∥AB，
∵EH?平面SAB，AB?平面SAB
∴EH∥平面SAB
∵SE：ED=BF：FC，EH∥DC
∴SH：HC=BF：FC，
∴HF∥BS
∵HF?平面SAB，BS?平面SAB
∴HF∥平面SAB
∵FH∩HE=H．
∴平面EHF∥平面SAB．
∵EF?平面EHF，
∴EF∥平面SAB．
点评：本题考查线面平行、面面平行的判定，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
桑基鱼塘是广东省珠江三角洲一种独具地方特色的农业生产形式．
如图所示，某学校的教学楼前有一块矩形空地ABCD，其长为32米，宽为18米，现要在此空地上种植一块矩形草坪，三边留有人行道，人行道宽度为a米与b米（a与b均不小于2米），且要求“转角处”（图中矩形AEFG）的面积为8平方米．
某建筑公司要在一块宽大的矩形地面（如图所示）上进行开发建设，阴影部分为一公共设施建设不能开发，且要求用栏栅隔开（栏栅要求在一直线上），公共设施边界为曲线f（x）=1-ax2（a＞0）的一部分，栏栅与矩形区域的边界交于点M、N，交曲线于点P，设P（t，f（t））．
