题目内容
当
时，函数
的最大值和最小值分别是（ ）A．
，
B．
，
C．
，
D．
，
【答案】分析：根据三角函数诱导公式，化简整理得f（x）=2sin（x+
）+
，结合正弦函数的单调性和
，即可算出函数f（x）的最大、最小值．
解答：解：∵sin（2π+x）=sinx，cos（2π-x）=cosx，sin（2013π+
）=-sin
=-
∴
=sinx+
cosx+
=2sin（x+
）+
∵
，得
∴-
≤sin（x+
）+≤1，得-1≤2sin（x+
）≤2
由此可得f（x）的最小值为-1+
=-
，最大值为2+
=
故选：A
点评：本题给出三角函数式，求函数的最大最小值，考查了三角函数诱导公式、正弦函数的图象与性质等知识，属于基础题．
）+，结合正弦函数的单调性和，即可算出函数f（x）的最大、最小值．解答：解：∵sin（2π+x）=sinx，cos（2π-x）=cosx，sin（2013π+
）=-sin=-∴
=sinx+cosx+=2sin（x+）+∵
，得∴-
≤sin（x+）+≤1，得-1≤2sin（x+）≤2由此可得f（x）的最小值为-1+
=-，最大值为2+=故选：A
点评：本题给出三角函数式，求函数的最大最小值，考查了三角函数诱导公式、正弦函数的图象与性质等知识，属于基础题．
练习册系列答案
相关题目
时，求函数的最大值和最小值；w.w.w.k.s.5.u.c.o.m 
在区间
上是单调函数，求实数
的取值范围，
的最小正周期和单调增区间；
时，函数
，
时，求
的值；
在
上是减函数，并求函数的最大值和最小值．
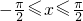时，函数
的最大值和最小值分别是
，
