题目内容
【题目】设函数![]() ,其中
,其中![]() .函数
.函数![]() 的图像在点
的图像在点![]() 处的切线与函数
处的切线与函数![]() 的图像在点
的图像在点![]() 处的切线互相垂直.
处的切线互相垂直.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
(Ⅰ)求f(x)的导函数,代入g(x),对函数g(x)求导,结合函数f(x)的图象在点A处的切线与g(x)的图象在点B处的切线互相垂直列式求t值;(Ⅱ)设函数F(x)=kg(x)﹣2f(x)=2kex(x+1)﹣2x2﹣8x﹣4,(x≥﹣2),求其导函数,分类求得函数最小值,可得k的取值范围.
(Ⅰ)由![]() 得,
得,![]() .
.
于是![]() ,所以
,所以![]() .
.
函数![]() 的图象在点
的图象在点![]() 处的切线与函数
处的切线与函数![]() 的图象在点
的图象在点![]() 处的切线互相垂直,所以
处的切线互相垂直,所以![]() ,即
,即![]()
![]()
(Ⅱ)![]() ,
,![]() .
.
设函数![]() =
=![]() (
(![]() ),
),
则![]() =
=![]() .
.
由题设可知![]() ,即
,即![]() .令
.令![]()
![]() 得
得![]()
![]() ,
,![]()
![]() .
.
(1)若![]() ,则
,则![]() ,此时
,此时![]() ,
,![]() ,
,![]() ,
,
![]() ,即
,即![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,所以
单调递增,所以![]() 在
在![]() 取
取
最小值![]() .
.
而![]()
![]()
![]() 当
当![]() 时,
时,![]() ,即
,即![]() 恒成立.
恒成立.
②若![]() 则
则![]() ,此时
,此时![]()
![]() 在
在![]() 单调递增,而
单调递增,而![]()
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,即
,即![]() 恒成立.
恒成立.
③若![]() 则
则![]() ,此时
,此时![]()
![]() .
.
![]() 当
当![]() 时,
时, ![]() 不能恒成立.
不能恒成立.
综上所述,![]() 的取值范围是
的取值范围是![]()

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
【题目】对某校高二年级800名学生上学期期末语文和外语成绩,按优秀和不优秀分类得结果:语文和外语都优秀的有60人,语文成绩优秀但外语不优秀的有140人,外语成绩优秀但语文不优秀的有100人.
问:(1)由题意列出学生语文成绩与外语成绩关系的![]() 列联表:
列联表:
语文优秀 | 语文不优秀 | 总计 | |
外语优秀 | |||
外语不优秀 | |||
总计 |
(2)能否在犯错概率不超过0.001的前提下认为该校学生的语文成绩与外语成绩有关系?(保留三位小数)
(附: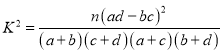 )
)
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |